Hallo Gunnar,

da Du deine Tangens-Lösung getwittert hast, und mein Bild eh schon der Katze eine Dreiecksrasur verpasst hat, kann ich sie auch aus dem Sack lassen.

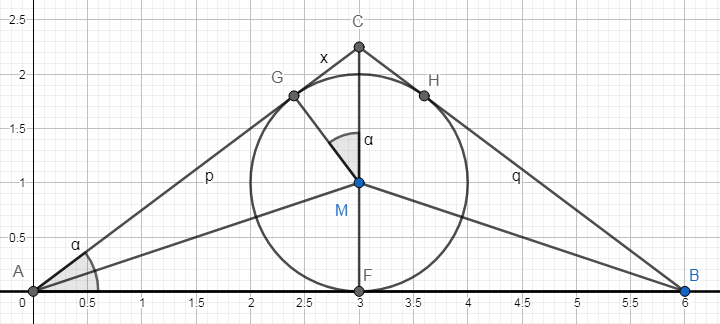
G und H sind die Berührpunkte des Inkreises mit den Seiten AC und CB. Sei h noch die Höhe FC des Dreiecks ABC (im Bild nicht bezeichnet).

Die Strecken AG und BH haben die Länge 3, weil AC/AB sowie BF/BC Tangenten aus dem gleichen Punkt sind. Die rechtwinkligen Drachen AFMG und BFMH (MH ist nicht gezeichnet) haben demnach jeweils die Fläche 3r = 3. Es bleibt die Frage nach dem verbleibenden kleinen Drachen MHCG. Bei diesem hat ein Seitenpaar die Länge r=1, die andere Seite x ist zu bestimmen.

Weil MG auf AC senkrecht steht und CF auf AB, sind die bei M und A gezeichneten Winkel gleich. Die rechtwinkligen Dreicke AFC und CGM sind damit ähnlich. Damit verhält sich

$$\displaystyle \frac{h}{3} = \frac{x}{1}$$

woraus folgt:

$$h=3x$$ (1)

Matthias Apsel schlug mir Pythagoras vor: $x²+1² = (h-1)²$, ich wollte aber auf Quadrate verzichten und wendete darum ein weiteres Verhältnis aus der Ähnlichkeit der Dreiecke an:

$$\displaystyle \frac{MC}{MG} = \frac{AC}{AF}$$

mit eingesetzten Werten

$$\displaystyle \frac{h-1}{1}=\frac{3+x}{3}$$ (2)

Einsetzen von (1) führt zu

$$\begin{aligned} & & 3x-1 &= 1+\frac{x}{3}
\Longleftrightarrow & & \frac{8}{3}x &= 2
\Longleftrightarrow & & x &= \frac{3}{4} \end{aligned}$$

Daraus berechnet sich die Fläche des kleinen Drachen zu 0,75.

Was aber eigentlich viel zu umständlich war. Wenn ich nämlich die Umkehrung von (1), also $$x=\frac{h}{3}$$, in (2) einsetze, bekomme ich $$\frac{h-1}{1}=\frac{3+\frac{h}{3}}{3} \Longleftrightarrow h-1=1+\frac{h}{9} \Longleftrightarrow \frac{8}{9}h=2 \Longleftrightarrow h=\frac{9}{4}$$, und daraus kann ich mit $$A=\frac{1}{2}\cdot 6 \cdot h = 3\cdot \frac{9}{4} = \frac{27}{4} = 6{,}75$$ die Fläche direkt berechnen, ohne große und kleine Drachen töten zu müssen.

Look Ma, no tangent!

Rolf

Wie groß ist die Fläche des gleichschenkligen Dreiecks mit Basis der Länge 6 und Inkreisradius 1?

Dann Poste ich auch meine Lösung, verwendet zwar auch den Tagens dieser wird aber nicht berechnet sonder nur Umgeformt.

Gesucht Fläche A: $$ A = H * \frac{B}2 $$ $$ B = 6 $$ $$ A = H * 3 $$ Winkelhalbierende führt auf den Winkel: $$ \alpha = 2 * arctan ( \frac{b}c ) = 2 * arctan ( \frac{1}3 ) $$ Das führt zur Höhe des Dreiecks: $$ H = \frac{B}2 * tan( 2 * arctan ( \frac{b}c ) ) $$ $$ H = 3 * tan( 2 * arctan ( \frac{b}c ) ) $$ Zu lösen: $$ tan( 2 * arctan ( \frac{b}c ) ) = \frac{d}e $$ Substitution: $$ \frac{d}e = m $$ $$ \frac{b}c = n $$ $$ a * arctan ( n ) = arctan( m ) $$ $$ 0 = arctan ( m ) - 2 * arctan( n ) $$ $$ 0 = arctan ( m ) - arctan( n ) - arctan( n )$$ $$ arctan( n ) = arctan ( m ) - arctan( n ) $$ $$ arctan( n ) = arctan ( m ) - arctan( n ) $$ $$ arctan( n ) = arctan ( \frac{m-n}{1+mn} ) $$ $$ n = \frac{m-n}{1+mn} $$ $$ 0 = mn^2+2n-m $$ Resubstitution: $$ 0 = \frac{d}e*\frac{b^2}{c^2}+2\frac{b}c-\frac{d}e $$ Einsetzen: $$ b = 1 $$ $$ c = 3 $$ $$ 0 = \frac{d}e*\frac{1^2}{3^2}+2\frac{1}3-\frac{d}e $$ $$ \frac{d}e-\frac{d}{9e} = \frac{2}3 $$ $$ \frac{8d}{9e} = \frac{2}3 $$ $$ \frac{d}e = \frac{3}4 $$ Und damit: $$ A = 3 * \frac{3}4 * 3 = 6,75 $$

Gruß
Jo

@@Gunnar Bittersmann

Quelle: https://twitter.com/panlepan/status/1155780397692858368

LLAP 🖖

Hallo Gunnar Bittersmann,

(1) Wie man leicht sieht, ist die Höhe des Dreiecks 2 + y.

(2) x + y = 1

(3) $\frac {2+y}{3} = \frac{x}{1}$

Aus (2) und (3) folgt y = 1/4.

Nur leider kann ich (1) nicht beweisen. 😡

Bis demnächst
Matthias