Mathematik zum Wochenende
- mathematik
Kleine Aufgabe zum Sonntag:
Ein Drittel des regulären Sechsecks ist schraffiert. Wie ist das Verhältnis a : b?
Kleine Aufgabe heißt: Wer mit Wurzeln oder Winkelfunktionen auffährt, macht die Aufgabe groß.
LLAP 🖖
Hi,
Ein Drittel des regulären Sechsecks ist schraffiert. Wie ist das Verhältnis a : b?
1 : 2
a ist die schraffierte Fläche, also 1/3, b die nicht-schraffierte, also 2/3 (ich hab die Gesamtfläche oBdA auf 1 gesetzt).
😉
cu,
Andreas a/k/a MudGuard
Hallo,
Ein Drittel des regulären Sechsecks ist schraffiert. Wie ist das Verhältnis a : b?
1 : 2
zu einfach. Ich nehme mal an, Gunnar meinte ein Drittel der Fläche des Sechsecks, nicht ein Drittel seiner Höhe. Das wäre ja trivial!
Schönen Sonntag noch,
Martin
Hi,
Ein Drittel des regulären Sechsecks ist schraffiert. Wie ist das Verhältnis a : b?
1 : 2
zu einfach. Ich nehme mal an, Gunnar meinte ein Drittel der Fläche des Sechsecks, nicht ein Drittel seiner Höhe.
Und eben deswegen stehen die Flächen a und b im Verhältnis 1 : 2 😉
cu,
Andreas a/k/a MudGuard
@@Der Martin
Ich nehme mal an, Gunnar meinte ein Drittel der Fläche des Sechsecks, nicht ein Drittel seiner Höhe.
Genau. Und a und b bezeichnen natürlich die Längen der Abschnitte auf der Achse, nicht die schraffierte bzw. nicht schraffierte Fläche.
LLAP 🖖
Hi,
Genau. Und a und b bezeichnen natürlich die Längen der Abschnitte auf der Achse, nicht die schraffierte bzw. nicht schraffierte Fläche.
Ach so. Sag das doch gleich, kann ja keiner ahnen … 😉
cu,
Andreas a/k/a MudGuard
Hallo,
Erinnere ich mich richtig, dass Strecken mit Kleinbuchstaben und Flächen mit Großbuchstaben bezeichnet werden?
Gruß
Kalk
Hallo Tabellenkalk,
Erinnere ich mich richtig, dass Strecken mit Kleinbuchstaben und Flächen mit Großbuchstaben bezeichnet werden?
Nö.
Strecken werden durch Anfangs- und Endpunkt benannt.
Bis demnächst
Matthias
Hallo,
Nö.
wohl eher ein Jein, oder?
Jedenfalls konnten weder a noch b niemals nicht für die Flächen stehen…
Gruß
Kalk
Hallo,
Erinnere ich mich richtig, dass Strecken mit Kleinbuchstaben und Flächen mit Großbuchstaben bezeichnet werden?
letzten Endes sind Namen (Bezeichnungen) Schall und Rauch. Es gibt gewisse Konventionen, aber ob du Strecken, Flächen, Volumina, Winkel etc. nun mit griechischen oder lateinischen Klein- oder Großbuchstaben bezeichnest, bleibt dir überlassen - wichtig ist nur, dass die Bezeichnungen klar und eindeutig sind.
- Punkte - Großbuchstaben
- Geraden - Kleinbuchstaben
- Flächen - Großbuchstaben
Strecken werden durch Anfangs- und Endpunkt benannt.
Strecken werden auch gern mit Kleinbuchstaben bezeichnet. Klassiker sind etwa a für die Seitenlänge eines Quadrats, r für den Radius eines Kreises oder h für die Höhe eines Dreiecks. Und der Satz des Pythagoras verwendet traditionell a, b, c, für die drei Seiten eines Dreiecks.
Ciao,
Martin
Hallo Der Martin,
Strecken werden auch gern mit Kleinbuchstaben bezeichnet. Klassiker sind etwa a für die Seitenlänge eines Quadrats, r für den Radius eines Kreises oder h für die Höhe eines Dreiecks. Und der Satz des Pythagoras verwendet traditionell a, b, c, für die drei Seiten eines Dreiecks.
Nein, mit den Kleinbuchstaben werden die Längen dieser Strecken bezeichnet. 😉
Bis demnächst
Matthias
@@Gunnar Bittersmann
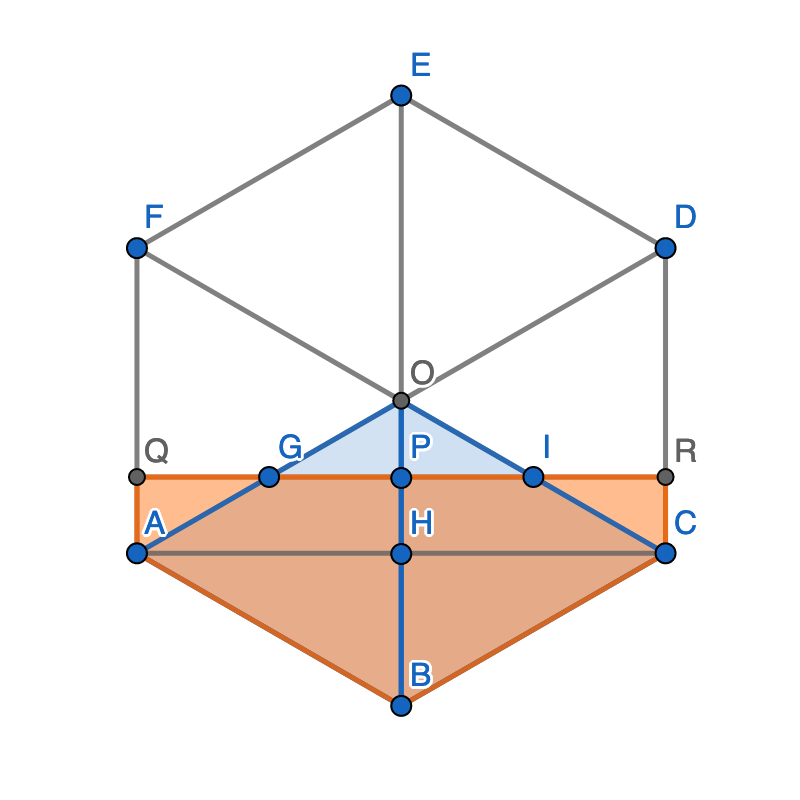
Wir teilen das Sechseck (Kantenlänge 1 o.B.d.A.) in 6 gleichseitige Dreiecke. Zwei davon (ABCO) haben ein Drittel der Fläche des Sechsecks.
G, H und I seien die Mittelpunkte von OA, OB und OC. Die Dreiecke AGQ und OGP sind kongruent nach WSW, damit OP = AQ = HP. Wegen OH = BH = ½ ist OP = ¼.
Ebenso sind die Dreiecke IOP und ICR kongruent. Damit sind ABCO und ABCRQ flächengleich; letzte ist also die schraffierte Fläche aus der Aufgabe.
BP : EP = (1 − ¼) : (1 + ¼) = 3 : 5
LLAP 🖖
Hallo,
Wir teilen das Sechseck (Kantenlänge 1 o.B.d.A.) in 6 gleichseitige Dreiecke. Zwei davon (ABCO) haben ein Drittel der Fläche des Sechsecks.
G, H und I seien die Mittelpunkte von OA, OB und OC. Die Dreiecke AGQ und OGP sind kongruent nach WSW, damit OP = AQ = HP. Wegen OH = BH = ½ ist OP = ¼.
Ebenso sind die Dreiecke IOP und ICR kongruent. Damit sind ABCO und ABCRQ flächengleich; letzte ist also die schraffierte Fläche aus der Aufgabe.
BP : EP = (1 − ¼) : (1 + ¼) = 3 : 5
genau so hatte ich es auch hergeleitet, nur dass ich mich auf eine Hälfte des Sechsecks beschränkt habe - es ist ja symmetrisch z.B. zur senkrechten Mittelachse.
So long,
Martin
PS: Was zum Geier heißt o.B.d.A.? Ohne Beißen des Autors?
Hallo Martin,
Ohne Beißen des Autors
😆😆😆 MMD
Vielleicht auch Ohne Besonders Dumme Annahmen...
Rolf
@@Der Martin
PS: Was zum Geier heißt o.B.d.A.? Ohne Beißen des Autors?
Ich beiße nicht. Ich verspreche aber auch nichts.
LLAP 🖖
Hallo Gunnar,
wenn man die Raute ABCO entlang AC teilt, halbiert man sie (weil der Höhenfußpunkt eines gleichseitigen Dreiecks die Seite, auf der er liegt, halbiert). ABC belegt demnach ein Sechstel des Secksecks, FDE aus Symmetriegründen auch und damit hat das Rechteck ACDF vier Sechstel der Sechseckfläche.
Um das untere Flächendrittel des Sechsecks zu bekommen, brauche ich ABC und ein weiteres Sechstel. Das erhalte ich durch das untere Viertel von ACDF, woraus (mit $\overline{AF}=1$) der Wert $\overline{HP}=\frac{1}{4}$ folgt. Daraus ergibt sich dann $\overline{BP}=3/4$ und $\overline{PE}=5/4$, das heißt:
$\displaystyle \frac{\overline{BP}}{\overline{PE}}=\frac{\frac{3}{4}}{\frac{5}{4}}=\frac{3}{5}$.
Rolf
@@Gunnar Bittersmann
Quelle: https://twitter.com/_WTProject/status/1160105638996975616
LLAP 🖖