nicht angemeldet
Gunnar Bittersmann@@Gunnar Bittersmann
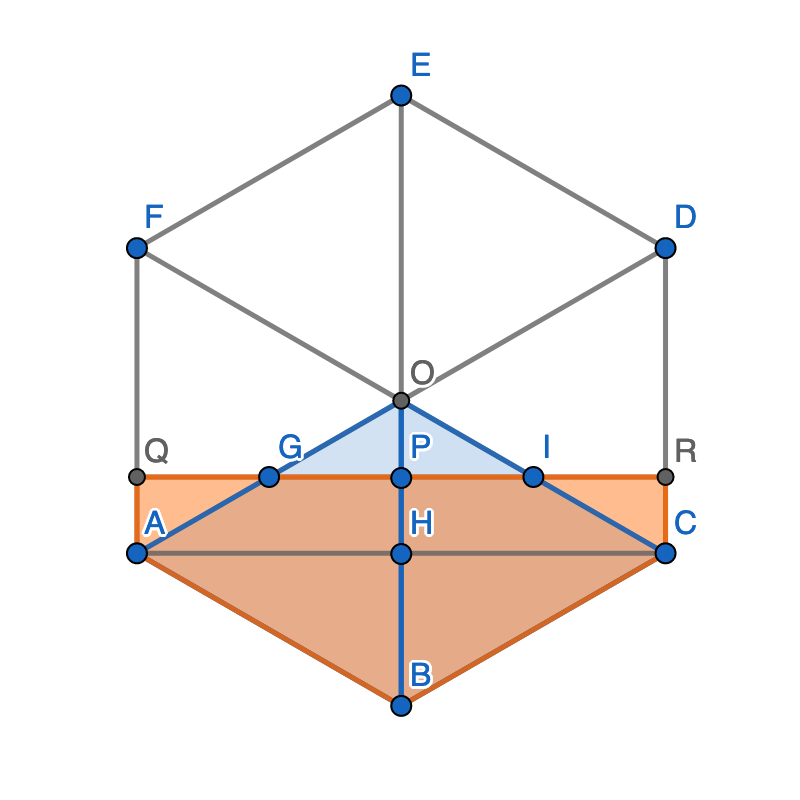
Wir teilen das Sechseck (Kantenlänge 1 o.B.d.A.) in 6 gleichseitige Dreiecke. Zwei davon (ABCO) haben ein Drittel der Fläche des Sechsecks.
G, H und I seien die Mittelpunkte von OA, OB und OC. Die Dreiecke AGQ und OGP sind kongruent nach WSW, damit OP = AQ = HP. Wegen OH = BH = ½ ist OP = ¼.
Ebenso sind die Dreiecke IOP und ICR kongruent. Damit sind ABCO und ABCRQ flächengleich; letzte ist also die schraffierte Fläche aus der Aufgabe.
BP : EP = (1 − ¼) : (1 + ¼) = 3 : 5
LLAP 🖖
--
„Man kann sich halt nicht sicher sein“, sagt der Mann auf der Straße, „dass in einer Gruppe Flüchtlinge nicht auch Arschlöcher sind.“
„Stimmt wohl“, sagt das Känguru, „aber immerhin kann man sich sicher sein, dass in einer Gruppe Rassisten nur Arschlöcher sind.“
—Marc-Uwe Kling
„Man kann sich halt nicht sicher sein“, sagt der Mann auf der Straße, „dass in einer Gruppe Flüchtlinge nicht auch Arschlöcher sind.“
„Stimmt wohl“, sagt das Känguru, „aber immerhin kann man sich sicher sein, dass in einer Gruppe Rassisten nur Arschlöcher sind.“
—Marc-Uwe Kling
MudGuard
Der Martin
Tabellenkalk
Matthias Apsel
Rolf B