@@Gunnar Bittersmann > Ist ja rege Beteiligung hier. Oh, es ist Leben in den Thread gekommen. Aber passt jemand auf? Nein! >  > > Damit gilt auch _KP_ = _ML_ und _MK_ = _LQ_. So weit, so gut. > Damit sind die Dreiecke _MPK_ und _MLQ_ kongruent Und wenn der _Topf_{: style="font-style: inherit; text-decoration: line-through"} Winkel ∠_BCA_ aber nun ein rechter ist? Dann liegen _M_, _K_ und _P_ auf einer Linie, ebenso _M_, _L_, und _Q_; es gibt also gar keine Dreiecke _MPK_ und _MLQ_. Von entarteten Dreiecken mit _φ_ = _ψ_ = 0 zu sprechen ist wohl nicht ganz sauber. Machen wir lieber eine Fallunterscheidung:  Nun ist ∠_PMQ_ ≡ ∠_KML_ = ∠_BCA_= 1∟, das Dreieck _MPQ_ ist somit rechtwinklig. _MP_ = _MK_ + _KP_ = _LQ_ + _ML_ = _MQ_. Das Dreieck _MPQ_ ist somit gleichschenklig. LLAP 🖖 -- _“I love to go to JS conferences to speak about how to avoid using JavaScript. Please learn CSS & HTML to reduce your JS code bloat.”_{: lang="en"} —Estelle Weyl

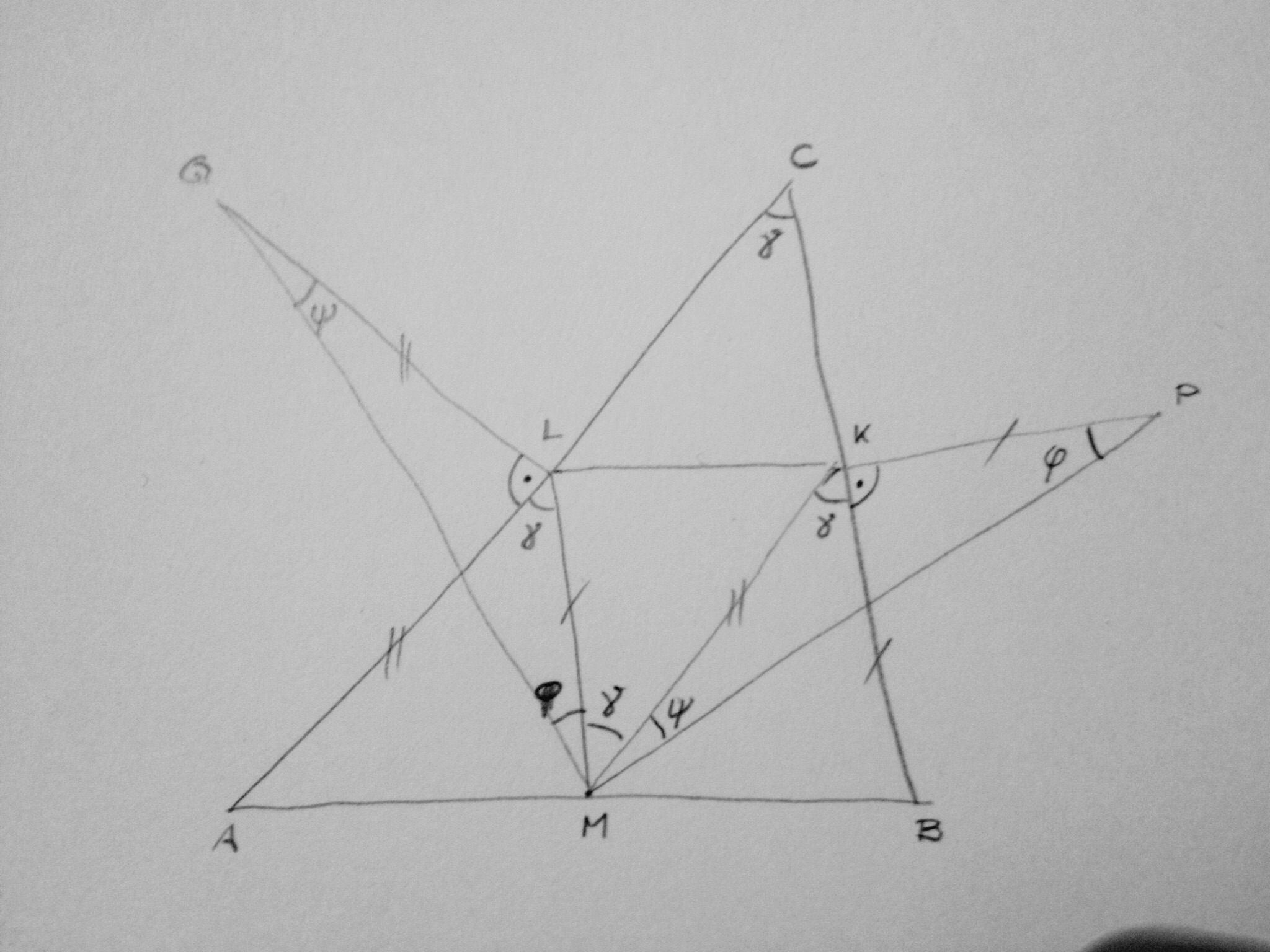
@@Gunnar Bittersmann > Ist ja rege Beteiligung hier. Oh, es ist Leben in den Thread gekommen. Aber passt jemand auf? Nein! >  > > Damit gilt auch _KP_ = _ML_ und _MK_ = _LQ_. So weit, so gut. > Damit sind die Dreiecke _MPK_ und _MLQ_ kongruent Und wenn der _Topf_{: style="font-style: inherit; text-decoration: line-through"} Winkel ∠_BCA_ aber nun ein rechter ist? Dann liegen _M_, _K_ und _P_ auf einer Linie, ebenso _M_, _L_, und _Q_; es gibt also gar keine Dreiecke _MPK_ und _MLQ_. Von entarteten Dreiecken mit _φ_ = _ψ_ = 0 zu sprechen ist wohl nicht ganz sauber. 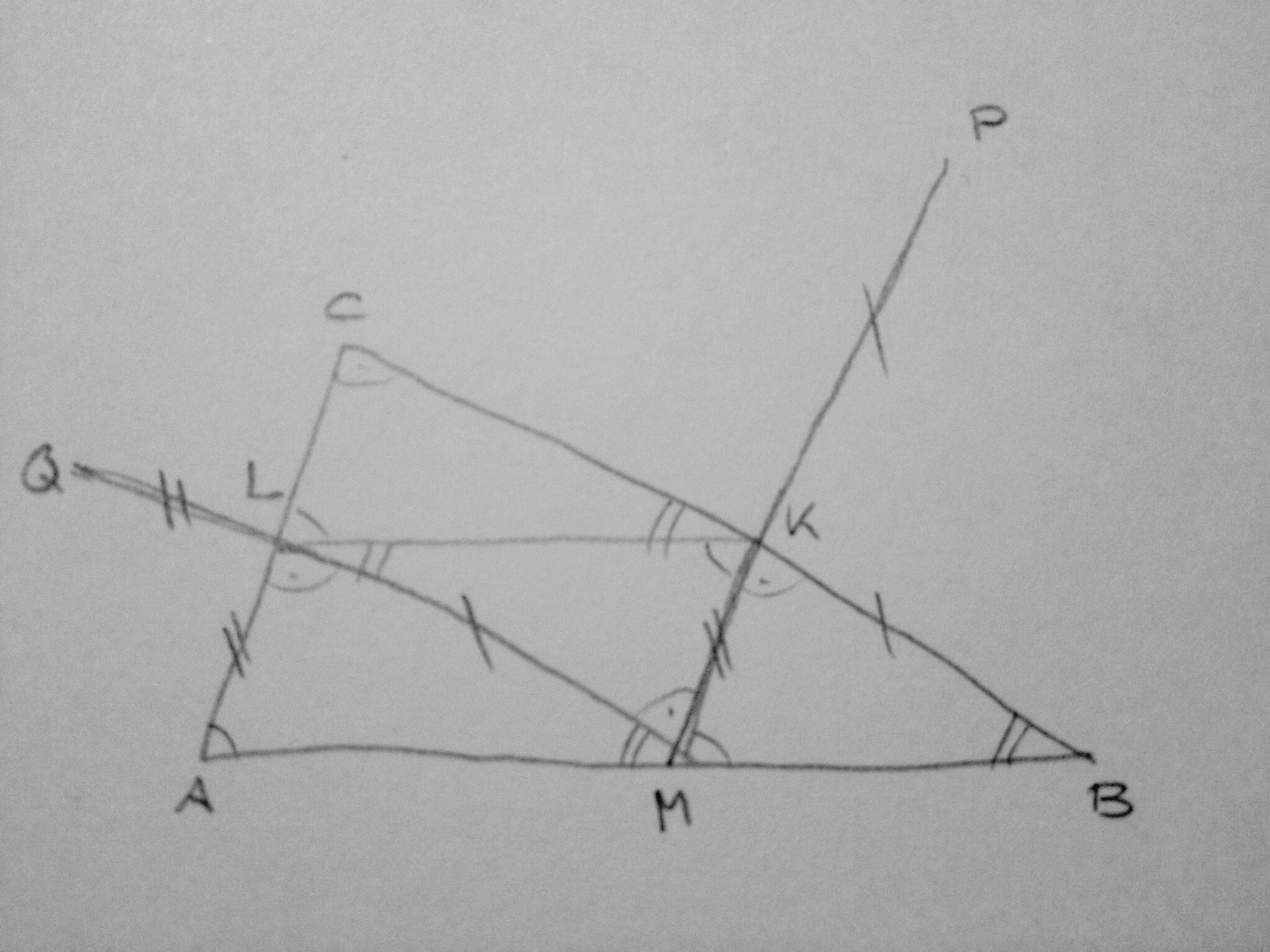Machen wir lieber eine Fallunterscheidung:  Nun ist ∠_PMQ_ ≡ ∠_KML_ = ∠_BCA_= 1∟, das Dreieck _MPQ_ ist somit rechtwinklig. _MP_ = _MK_ + _KP_ = _LQ_ + _ML_ = _MQ_. Das Dreiceck _MPQ_ ist somit gleichschenklig. LLAP 🖖 -- _“I love to go to JS conferences to speak about how to avoid using JavaScript. Please learn CSS & HTML to reduce your JS code bloat.”_{: lang="en"} —Estelle Weyl

@@Gunnar Bittersmann > Ist ja rege Beteiligung hier. Oh, es ist Leben in den Thread gekommen. Aber passt jemand auf? Nein! >  > > Damit gilt auch _KP_ = _ML_ und _MK_ = _LQ_. So weit, so gut. > Damit sind die Dreiecke _MPK_ und _MLQ_ kongruent Und wenn der _Topf_{: style="font-style: inherit; text-decoration: line-through"} Winkel ∠_BCA_ aber nun ein rechter ist? Dann liegen _M_, _K_ und _P_ auf einer Linie, ebenso _M_, _L_, und _Q_; es gibt also gar keine Dreiecke _MPK_ und _MLQ_. Von entarteten Dreiecken mit _φ_ = _ψ_ = 0 zu sprechen ist wohl nicht ganz sauber. Machen wir lieber eine Fallunterscheidung: Skizze Nun ist ∠_PMQ_ ≡ ∠_KML_ = ∠_BCA_= 1∟, das Dreieck _MPQ_ ist somit rechtwinklig. _MP_ = _MK_ + _KP_ = _LQ_ + _ML_ = _MQ_. Das Dreiceck _MPQ_ ist somit gleichschenklig. LLAP 🖖 -- _“I love to go to JS conferences to speak about how to avoid using JavaScript. Please learn CSS & HTML to reduce your JS code bloat.”_{: lang="en"} —Estelle Weyl