Mathematik zum Wochenende - Auflösung Teil 3
bearbeitet vonHallo Matthias Apsel,
> Geht das auch ohne Kenntnis von _q_?
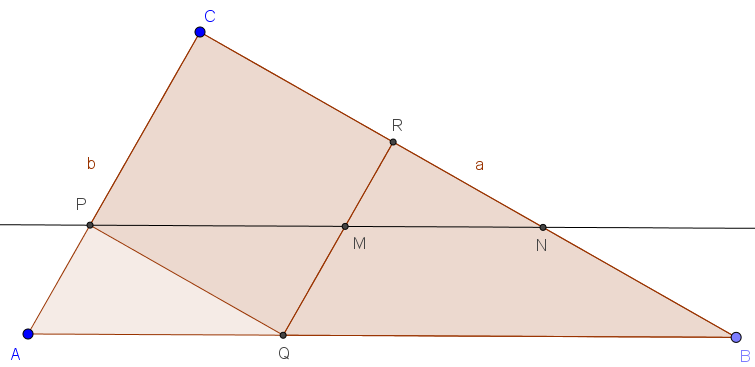
Das Dreieck _ABC_ wird gebildet durch das Quadrat _PQRC_ und die beiden ähnlichen Dreiecke _QBR_ und _AQP_. Ohne Beschränkung der Allgemeinheit sei _a_ > _b_.
Als Hilflinie verwenden wir eine Parallele zur Hypotenuse _c_ durch den Punkt _P_.
Die Dreiecke _AQP_ und _MPQ_ sind kongruent, ebenso die Dreiecke _QBR_ und _PNC_.
Das Dreieck _PNC_ ist größer als das Trapez _PMRC_ (wegen _a_ > _b_ ist auch _CN_ > _CR_, mithin liegt _R_ zwischen _C_ und _N_, wegen der Parallelität von _PC_ und _MR_ liegt _M_ zwischen _P_ und _N_)
Damit sind die Dreiecke _QBR_ und _AQP_ stets größer als das Quadrat.
Für das gleichschenklig-rechtwinklige Dreieck _ABC_ wären _P_ und _N_ die Mittelpunkte der Katheten und _Q_ der Mittelpunkt der Hypothenuse. Verbindet man die Mittelpunkte der Seiten eines Dreicks, so entstehen vier kongruente Dreiecke, zwei davon bilden das Quadrat. In diesem Fall ist das Quadrat also halb so groß wie das Dreieck _ABC_.
Bis demnächst
Matthias
--
Dieses Forum nutzt Markdown. Im [Wiki](https://wiki.selfhtml.org){: style="color:#3481cd"} erhalten Sie [Hilfe bei der Formatierung Ihrer Beiträge](https://wiki.selfhtml.org/wiki/SELFHTML:Forum/Formatierung_der_Beitr%C3%A4ge){: style="color:#3481cd"}.
Mathematik zum Wochenende - Auflösung Teil 3
bearbeitet vonHallo Matthias Apsel,
> Geht das auch ohne Kenntnis von _q_?

Das Dreieck _ABC_ wird gebildet durch das Quadrat _PQRC_ und die beiden ähnlichen Dreiecke _QBR_ und _AQP_. Ohne Beschränkung der Allgemeinheit sei _a_ > _b_.
Als Hilflinie verwenden wir eine Parallele zur Hypothenuse _c_ durch den Punkt _P_.
Die Dreiecke _AQP_ und _MPQ_ sind kongruent, ebenso die Dreiecke _QBR_ und _PNC_.
Das Dreieck _PNC_ ist größer als das Trapez _PMRC_ (wegen _a_ > _b_ ist auch _CN_ > _CR_, mithin liegt _R_ zwischen _C_ und _N_, wegen der Parallelität von _PC_ und _MR_ liegt _M_ zwischen _P_ und _N_)
Damit sind die Dreiecke _QBR_ und _AQP_ stets größer als das Quadrat.
Für das gleichschenklig-rechtwinklige Dreieck _ABC_ wären _P_ und _N_ die Mittelpunkte der Katheten und _Q_ der Mittelpunkt der Hypothenuse. Verbindet man die Mittelpunkte der Seiten eines Dreicks, so entstehen vier kongruente Dreiecke, zwei davon bilden das Quadrat. In diesem Fall ist das Quadrat also halb so groß wie das Dreieck _ABC_.
Bis demnächst
Matthias
--
Dieses Forum nutzt Markdown. Im [Wiki](https://wiki.selfhtml.org){: style="color:#3481cd"} erhalten Sie [Hilfe bei der Formatierung Ihrer Beiträge](https://wiki.selfhtml.org/wiki/SELFHTML:Forum/Formatierung_der_Beitr%C3%A4ge){: style="color:#3481cd"}.
Mathematik zum Wochenende - Auflösung Teil 3
bearbeitet vonHallo Matthias Apsel,
> Geht das auch ohne Kenntnis von _q_?

Das Dreieck _ABC_ wird gebildet durch das Quadrat _PQRC_ und die beiden ähnlichen Dreiecke _QBR_ und _AQP_. Ohne Beschränkung der Allgemeinheit sei _a_ > _b_.
Als Hilflinie verwenden wir ein Parallele zur Hypothenuse _c_ durch den Punkt _P_.
Die Dreiecke _AQP_ und _MPQ_ sind kongruent, ebenso die Dreiecke _QBR_ und _PNC_.
Das Dreieck _PNC_ ist größer als das Trapez _PMRC_ (wegen _a_ > _b_ ist auch _CN_ > _CR_, mithin liegt _R_ zwischen _C_ und _N_, wegen der Parallelität von _PC_ und _MR_ liegt _M_ zwischen _P_ und _N_)
Damit sind die Dreiecke _QBR_ und _AQP_ stets größer als das Quadrat.
Für das gleichschenklig-rechtwinklige Dreieck _ABC_ wären _P_ und _N_ die Mittelpunkte der Katheten und _Q_ der Mittelpunkt der Hypothenuse. Verbindet man die Mittelpunkte der Seiten eines Dreicks, so entstehen vier kongruente Dreiecke, zwei davon bilden das Quadrat. In diesem Fall ist das Quadrat also halb so groß wie das Dreieck _ABC_.
Bis demnächst
Matthias
--
Dieses Forum nutzt Markdown. Im [Wiki](https://wiki.selfhtml.org){: style="color:#3481cd"} erhalten Sie [Hilfe bei der Formatierung Ihrer Beiträge](https://wiki.selfhtml.org/wiki/SELFHTML:Forum/Formatierung_der_Beitr%C3%A4ge){: style="color:#3481cd"}.
Mathematik zum Wochenende
bearbeitet vonHallo Matthias Apsel,
> Geht das auch ohne Kenntnis von _q_?

Das Dreieck _ABC_ wird gebildet durch das Quadrat _PQRC_ und die beiden ähnlichen Dreiecke _QBR_ und _AQP_. Ohne Beschränkung der Allgemeinheit sei _a_ > _b_.
Als Hilflinie verwenden wir ein Parallele zur Hypothenuse _c_ durch den Punkt _P_.
Die Dreiecke _AQP_ und _MPQ_ sind kongruent, ebenso die Dreiecke _QBR_ und _PNC_.
Das Dreieck _PNC_ ist größer als das Trapez _PMRC_ (wegen _a_ > _b_ ist auch _CN_ > _CR_, mithin liegt _R_ zwischen _C_ und _N_, wegen der Parallelität von _PC_ und _MR_ liegt _M_ zwischen _P_ und _N_)
Damit sind die Dreiecke _QBR_ und _AQP_ stets größer als das Quadrat.
Für das gleichschenklig-rechtwinklige Dreieck _ABC_ wären _P_ und _N_ die Mittelpunkte der Katheten und _Q_ der Mittelpunkt der Hypothenuse. Verbindet man die Mittelpunkte der Seiten eines Dreicks, so entstehen vier kongruente Dreiecke, zwei davon bilden das Quadrat. In diesem Fall ist das Quadrat also halb so groß wie das Dreieck _ABC_.
Bis demnächst
Matthias
--
Dieses Forum nutzt Markdown. Im [Wiki](https://wiki.selfhtml.org){: style="color:#3481cd"} erhalten Sie [Hilfe bei der Formatierung Ihrer Beiträge](https://wiki.selfhtml.org/wiki/SELFHTML:Forum/Formatierung_der_Beitr%C3%A4ge){: style="color:#3481cd"}.


