Mathematik zum Wochenanfang – noch ein Lösungsansatz

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Ich hatte es auch so wie ottogals zweite Lösung. Naja, jedenfalls auf dem Papier für b und d. Mir war klar, dass das für die andere Mittelsenkrechte auch für a und c gilt; ich hätte nur noch mal genau hinkucken und das aufschreiben müssen.

Ich hab noch einen anderen Lösungsansatz für die Fälle 1 bis 3 sowie Fall 5:

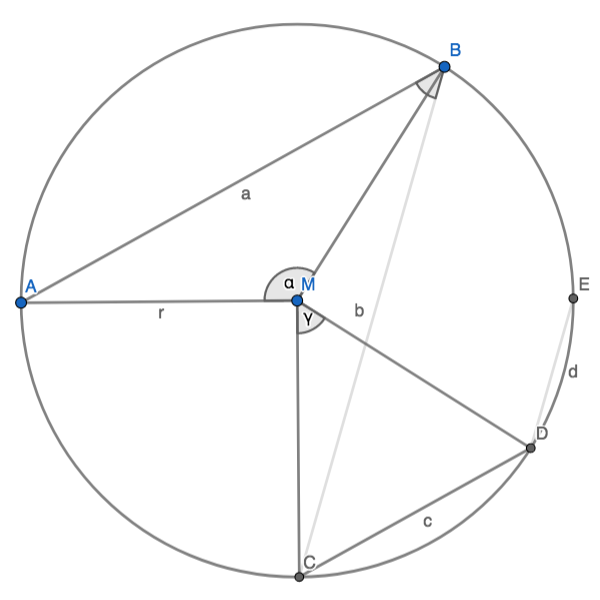
∠AMC = ∠BMD = 1∟ hatten wir ja schon.

α = ∠AMB, γ = ∠CMD; α + γ = π

Cosinussatz in △ABM: (1) a² = 2r² − 4r² cos α

und in △CDM: (2) c² = 2r² − 4r² cos γ = 2r² − 4r² cos(π − α) = 2r² + 4r² cos α

(1) + (2) ergibt a² + c² = 4r²

Das lässt sich auf diesem Weg sicher auch für b und d zeigen.

LLAP 🖖