Mathematik zum Wochenende – Lösung
bearbeitet von@@Gunnar Bittersmann
> Na dann warte ich noch ein wenig mit der Auflösung.
So, genug gewartet. @encoder sollte die Lösung inzwischen gefunden haben – sie geht genauso wie seine/ihre [Lösung vom Februar](https://forum.selfhtml.org/self/2018/feb/21/mathematik-zur-wochenmitte/1714720#m1714720):
{:width="408"}
Wir zerlegen das Quadrat *EBFG* mit Parallelen zu *AB* und *AD* in 4 Dreiecke und ein Quadrat.
Mit *AB* = 4 und *AE* = *a* ergibt sich für den Flächeninhalt von *EBFG*:
17 = 4 × ½ × 4*a* + (4 − *a*)² = 8*a* + 16 − 8*a* + *a*²
17 = 16 + *a*²
Das ist genau das, was einem mit Pythagoras auch ins Auge springt, nur eben ohne.
*AE* = *a* = 1.
{:width="504"}
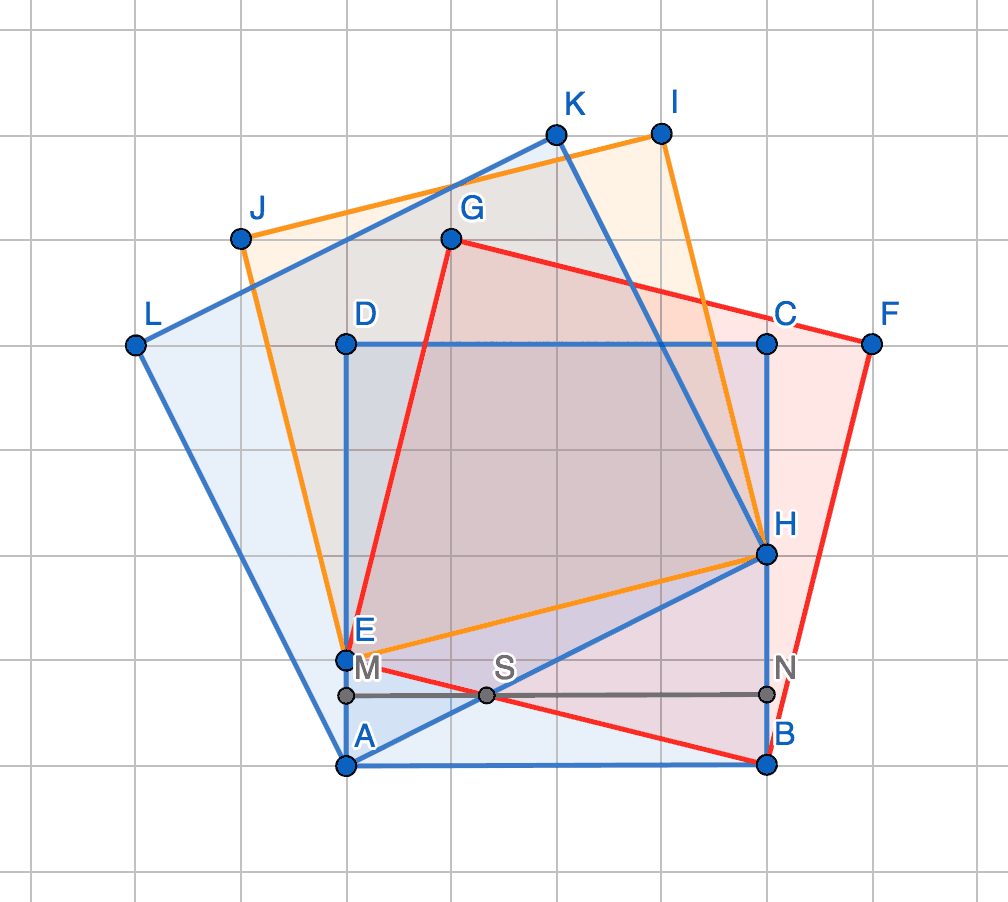
Analog lässt sich so über den Flächeninhalt von *AHKL* auch *BH* = *b* bestimmen:
20 = 4 × ½ × 4*b* + (4 − *b*)² = 8*b* + 16 − 8*b* + *b*² = 16 + *b*²
*BH* = *b* = 2
Darauf kommt man aber auch über *EB* = *EH* wegen der Flächengleichheit von *EBFG* und *EHIJ*.
*S* Schnittpunkt von *AH* und *EB*, *M*, *N* Fußpunkte der Lote von *S* auf *AE* und *BH*
Die Dreiecke *SEA* und *SBH* sind änhlich. (Die Innenwinkel sind Scheitelwinkel bzw. Wechselwinkel an geschnittenen Parallelen.)
*SM* : *SN* = *AE* : *BH* = 1 : 2, wegen *SM* + *SN* = 4 ist *SM* = ⁴⁄₃
Flächeninhalt von *SEA* ist ½ × 1 × ⁴⁄₃ = ⅔, Flächeninhalt von *SBH* ist 4mal so groß.
Die gesuchte Differenz der Flächen ist demnach 3 × ⅔ = 2.
---
{:width="504"}
Zusatzaufgaben: Wir legen ein Koordinatensystem so, dass *A* im Ursprung liegt und *D*(0, 4) ist.
Dann ist *E*(0, 1) und *G*(1, 5) sowie *H*(4, 2) und *I*(3, 6), *K*(2, 6), *L*(−2, 4).
Man sieht, dass *D*, *G* und *K* auf einer Linie liegen und dass *DG* = *GK* ist.
Die Gerade *GI* hat den Anstieg ½, ebenso wie die Gerade *LK*, sie sind also parallel.
Hat jemand eine Lösung ohne Rechnen mit Koordinaten, sondern rein geometrisch?
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann
Mathematik zum Wochenende – Lösung
bearbeitet von@@Gunnar Bittersmann
> Na dann warte ich noch ein wenig mit der Auflösung.
So, genug gewartet. @encoder sollte die Lösung inzwischen gefunden haben – sie geht genauso wie seine/ihre [Lösung vom Februar](https://forum.selfhtml.org/self/2018/feb/21/mathematik-zur-wochenmitte/1714720#m1714720):
{:width="408"}
Wir zerlegen das Quadrat *EBFG* mit Parallelen zu *AB* und *AD* in 4 Dreiecke und ein Quadrat.
Mit *AB* = 4 und *AE* = *a* ergibt sich für den Flächeninhalt von *EBFG*:
17 = 4 × ½ × 4*a* + (4 − *a*)² = 8*a* + 16 − 8*a* + *a*²
17 = 16 + *a*²
Das ist genau das, was einem mit Pythagoras auch ins Auge springt, nur eben ohne.
*AE* = *a* = 1.
{:width="504"}
Analog lässt sich so über den Flächeninhalt von *AHKL* auch *BH* = *b* bestimmen:
20 = 4 × ½ × 4*b* + (4 − *b*)² = 8*b* + 16 − 8*b* + *b*² = 16 + *b*²
*BH* = *b* = 2
Darauf kommt man aber auch über *EB* = *EH* wegen der Flächengleichheit von *EBFG* und *EHIJ*.
*S* Schnittpunkt von *AH* und *EB*, *M*, *N* Fußpunkte der Lote von *S* auf *AE* und *BH*
Die Dreiecke *SEA* und *SBH* sind änhlich. (Die Innenwinkel sind Scheitelwinkel bzw. Wechselwinkel an geschnittenen Parallelen.)
*SM* : *SN* = *AE* : *BH* = 1 : 2, wegen *SM* + *SN* = 4 ist *SM* = ⁴⁄₃
Flächeninhalt von *SEA* ist ½ × 1 × ⁴⁄₃ = ⅔, Flächeninhalt von *SBH* ist 4mal so groß.
Die gesuchte Differenz der Flächen ist demnach 3 × ⅔ = 2.
---
{:width="504"}
Zusatzaufgaben: Wir legen ein Koordinatensystem so, dass *A* im Ursprung liegt und *D*(0, 4) ist.
Dann ist *E*(0, 1) und *G*(1, 5) sowie *H*(4, 2) und *I*(3, 6), *K*(2, 6), *L*(−2, 4).
Man sieht, dass *D*, *G* und *K* auf einer Linie liegen und dass *DG* = *GK* ist.
Die Gerade *GI* hat den Anstieg ½, ebenso wie die Gerade *LK*, sie sind also parallel.
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann
Mathematik zum Wochenende
bearbeitet von@@Gunnar Bittersmann
> Na dann warte ich noch ein wenig mit der Auflösung.
So, genug gewartet. @encoder sollte die Lösung inzwischen gefunden haben – sie geht genauso wie seine/ihre [Lösung vom Februar](https://forum.selfhtml.org/self/2018/feb/21/mathematik-zur-wochenmitte/1714720#m1714720):
{:width="408"}
Wir zerlegen das Quadrat *EBFG* mit Parallelen zu *AB* und *AD* in 4 Dreiecke und ein Quadrat.
Mit *AB* = 4 und *AE* = *a* ergibt sich für den Flächeninhalt von *EBFG*:
17 = 4 × ½ × 4*a* + (4 − *a*)² = 8*a* + 16 − 8*a* + *a*²
17 = 16 + *a*²
Das ist genau das, was einem mit Pythagoras auch ins Auge springt, nur eben ohne.
*AE* = *a* = 1.
{:width="504"}
Analog lässt sich so über den Flächeninhalt von *AHKL* auch *BH* = *b* bestimmen:
20 = 4 × ½ × 4*b* + (4 − *b*)² = 8*b* + 16 − 8*b* + *b*² = 16 + *b*²
*BH* = *b* = 2
Darauf kommt man aber auch über *EB* = *EH* wegen der Flächengleichheit von *EBFG* und *EHIJ*.
*S* Schnittpunkt von *AH* und *EB*, *M*, *N* Fußpunkte der Lote von *S* auf *AE* und *BH*
Die Dreiecke *SEA* und *SBH* sind änhlich. (Die Innenwinkel sind Scheitelwinkel bzw. Wechselwinkel an geschnittenen Parallelen.)
*SM* : *SN* = *AE* : *BH* = 1 : 2, wegen *SM* + *SN* = 4 ist *SM* = ⁴⁄₃
Flächeninhalt von *SEA* ist ½ × 1 × ⁴⁄₃ = ⅔, Flächeninhalt von *SBH* ist 4mal so groß.
Die gesuchte Differenz der Flächen ist demnach 3 × ⅔ = 2.
---
{:width="504"}
Zusatzaufgaben: Wir legen ein Koordinatensystem so, dass *A* im Ursprung liegt und *D*(0, 4) ist.
Dann ist *E*(0, 1) und *G*(1, 5) sowie *H*(4, 2) und *I*(3, 6), *K*(2, 6), *L*(−2, 4).
Man sieht, dass *D*, *G* und *K* auf einer Linie liegen und dass *DG* = *GK* ist.
Die Gerade *GI* hat den Anstieg ½, ebenso wie die Gerade *LK*, sie sind also parallel.
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann


