Mathematik zum Wochenende – Lösung

[Gunnar Bittersmann]

@@Tabellenkalk

Dann habe ich gerade noch mal in den Twitterkanal geschaut - die Antwort von Mathmorphosis ist beschämend einfach.

Wieso hab ich das nicht gesehen??

Wenn’s dich tröstet: Ich auch nicht. Meh.

Den Kreis einzuzeichnen war dann doch keine so gute Idee; der lenkt nur ab.

Er hätte allerdings die Kongruenz noch begründen können.

Mein Reden. Wer sagt denn, dass nach dem Umklappen die drei Punkte auf einer Graden liegen? Dafür brauchts die 45°.

Nein, überhaupt nicht.

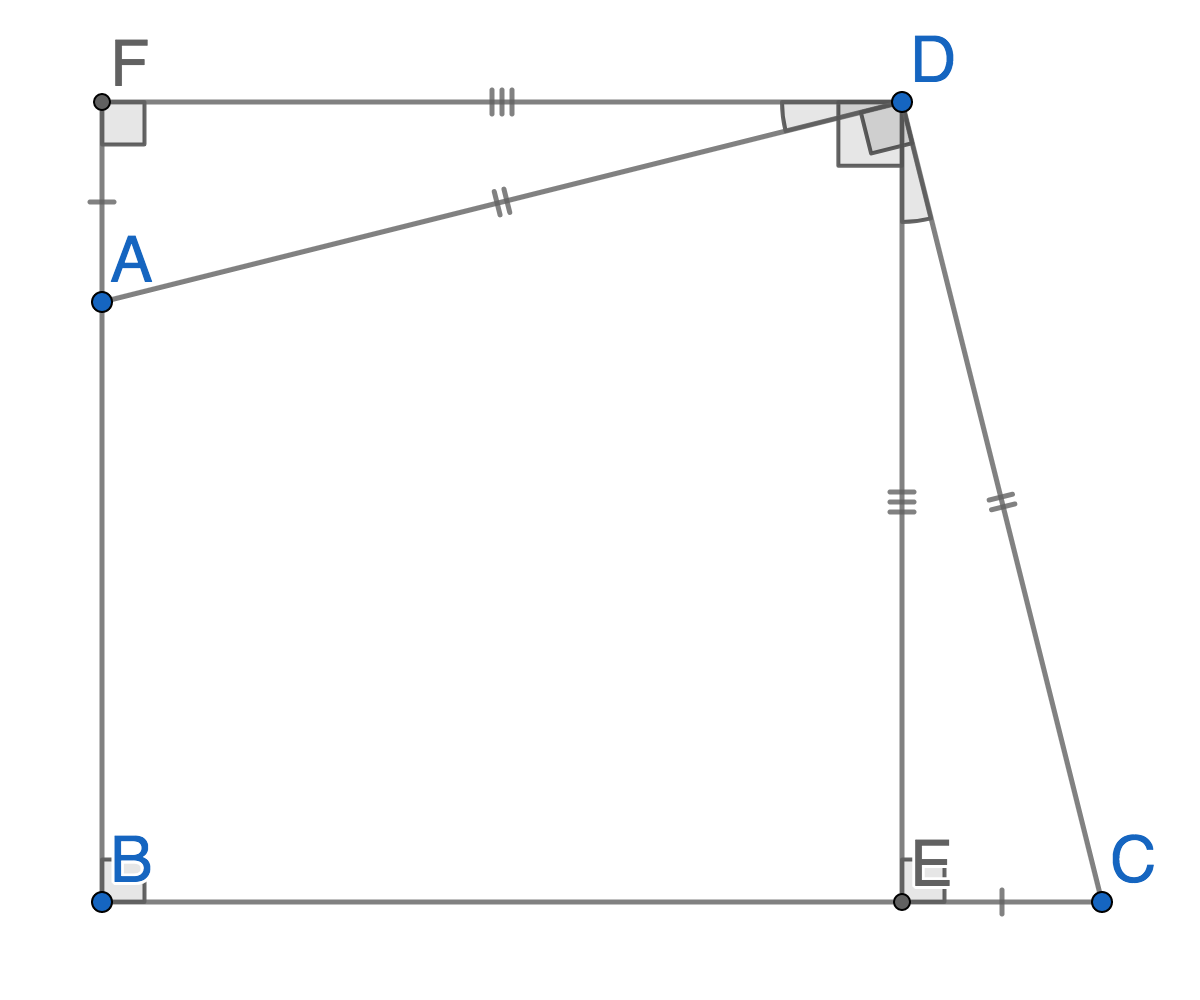
E Fußpunkt des Lotes von D auf BC, F Fußpunkt des Lotes von D auf AB, also ∠CED = ∠AFD = 1∟.

∠ADC = 1∟ gegeben, damit ∠EDC = ∠ADC − ∠ADE = 1∟ − ∠ADE.

Wegen AB ⟂ BC ist auch DE ⟂ DF, damit ∠FDA = ∠FDE − ∠ADE = 1∟ − ∠ADE; d.h. ∠EDC = ∠FDA.

Außerdem DC = DA (gegeben), damit △ECD ≅ △FAD nach WSW.

Daraus folgt EC = FA und DE = DF.

Wegen letzterem und der rechten Winkel ist BEDF ein Quadrat, flächengleich zu ABCD 64cm², demzufolge DE = DF = FB = BE = 8cm.

BC = 10cm (gegeben), FA = EC = BC − BE = 10cm − 8cm = 2cm.

AB = FB − FA = 8cm − 2cm = 6cm.

LLAP 🖖