Geometrie zur Wochenmitte – Lösung
bearbeitet von@@Rolf B
> sorry. Ich bin einfach zu dumm, um eine Logikkette wie in deiner Lösung zu konstruieren, ohne mir dabei in irgendwelche Gliedmaßen zu schießen 😉
Wenn das zu einer eleganteren Lösung führt, ist diese Dummheit in Wahrheit Klugheit.
Magst du deine Lösung selbst präsentieren oder soll ich?
> Immerhin haben wir $$\sin{30°}=\frac{1}{2}$$ auf die gleiche Art konstruiert 😀
Jetzt nicht mehr; der 30°-Winkel ist weg – @ottogal hat noch eine Abkürzung gefunden. Ein Wort gab das andere und mit vereinten Kräften entstand diese Lösung:
{:width="400"}
Seien *a* = *AB*; *I*, *J*, *K*, *L* die Eckpunkte des innerern Quadrats; *O* der Mittelpunkt von *ABCD* und *IJKL*[^symm]; *M* der Mittelpunkt von *AB*.
Da △*ABI* rechtwinklig ist, liegt *I* auf dem Thaleskreis um *M*, folglich *MI* = *MB* und damit ∠*MIB* = ∠*IBM* = 15°. Nach Außenwinkelsatz ist ∠*IMA* = 30°. Wegen *MO* ⟂ *AB* ist ∠*OMI* = 60°.
Da auch *MI* = *MO*, ist △*IMO* gleichseitig; also auch *IO* = ½*a* und damit *IK* = *a*. Die Diagonalen des inneren Quadrats *IJKL* sind so lang wie die Seiten des äußeren Quadrats *ABCD*.
Das innere Quadrat so gedreht, dass die Eckpunkte auf den Seiten des äußeren liegen:
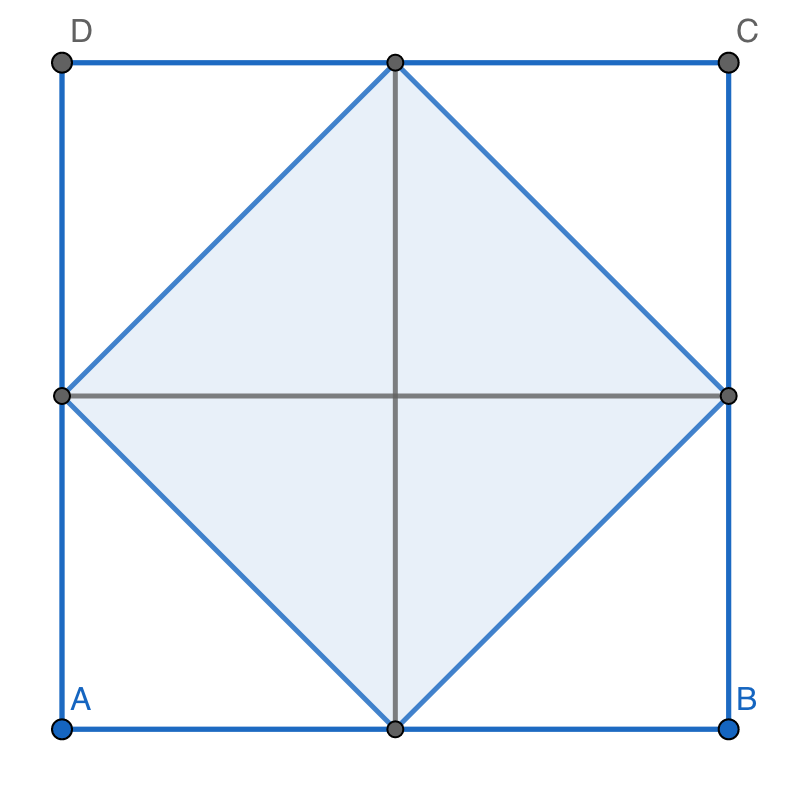{:width="400"}
Wie man leicht sieht (hier aber wirklich!), ist das innere Quadrat halb so groß wie das äußere, also ½*a*². Mit *a* = 10 cm ergeben sich 50 cm².
[^symm]: Aus Symmetriegründen fallen die Mittelpunkte von *ABCD* und *IJKL* zusammen.
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann
Geometrie zur Wochenmitte – Lösung
bearbeitet von@@Rolf B
> sorry. Ich bin einfach zu dumm, um eine Logikkette wie in deiner Lösung zu konstruieren, ohne mir dabei in irgendwelche Gliedmaßen zu schießen 😉
Wenn das zu einer eleganteren Lösung führt, ist diese Dummheit in Wahrheit Klugheit.
Magst du deine Lösung selbst präsentieren oder soll ich?
> Immerhin haben wir $$\sin{30°}=\frac{1}{2}$$ auf die gleiche Art konstruiert 😀
Jetzt nicht mehr; der 30°-Winkel ist weg – @ottogal hat noch eine Abkürzung gefunden. Ein Wort gab das andere und mit vereinten Kräften entstand diese Lösung:
{:width="400"}
Seien *a* = *AB*; *I*, *J*, *K*, *L* die Eckpunkte des innerern Quadrats; *O* der Mittelpunkt von *ABCD* und *IJKL*[^symm]; *M* der Mittelpunkt von *AB*.
Da △*ABI* rechtwinklig ist, liegt *I* auf dem Thaleskreis um *M*, folglich *MI* = *MB* und damit ∠*MIB* = ∠*IBM* = 15°. Nach Außenwinkelsatz ist ∠*IMA* = 30°. Wegen *MO* ⟂ *AB* ist ∠*OMI* = 60°.
Da auch *MI* = *MO*, ist △*IMO* gleichseitig; also *IO* = ½*a* und damit *IK* = *a*. Die Diagonalen des inneren Quadrats *IJKL* sind so lang wie die Seiten des äußeren *ABCD*.
Das innere Quadrat so gedreht, dass die Eckpunkte auf den Seiten des äußeren liegen:
{:width="400"}
Wie man leicht sieht (hier aber wirklich!), ist das innere Quadrat halb so groß wie das äußere, also ½*a*². Mit *a* = 10 cm ergeben sich 50 cm².
[^symm]: Aus Symmetriegründen fallen die Mittelpunkte von *ABCD* und *IJKL* zusammen.
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann
Geometrie zur Wochenmitte – Lösung
bearbeitet von@@Rolf B
> sorry. Ich bin einfach zu dumm, um eine Logikkette wie in deiner Lösung zu konstruieren, ohne mir dabei in irgendwelche Gliedmaßen zu schießen 😉
Wenn das zu einer eleganteren Lösung führt, ist diese Dummheit in Wahrheit Klugheit.
Magst du deine Lösung selbst präsentieren oder soll ich?
> Immerhin haben wir $$\sin{30°}=\frac{1}{2}$$ auf die gleiche Art konstruiert 😀
Jetzt nicht mehr; der 30°-Winkel ist weg – @ottogal hat noch eine Abkürzung gefunden. Ein Wort gab das andere und mit vereinten Kräften entstand diese Lösung:
{:width="400"}
Seien *a* = *AB*; *I*, *J*, *K*, *L* die Eckpunkte des innerern Quadrats; *O* der Mittelpunkt von *ABCD* und *IJKL*[^symm]; *M* der Mittelpunkt von *AB*.
Da △*ABI* rechtwinklig ist, liegt *I* auf dem Thaleskreis um *M*, folglich *MI* = *MB* und damit ∠*MIB* = ∠*IBM* = 15°. Nach Außenwinkelsatz ist ∠*IMA* = 30°. Wegen *MO* ⟂ *AB* ist ∠*OMI* = 60°.
Da auch *MI* = *MO*, ist △*IMO* gleichseitig; also *IO* = ½*a* und damit *IK* = *a*. Die Diagonalen des inneren Quadrats *IJKL* sind so lang wie die Seiten des äußeren *ABCD*.
Das innere Quadrat so gedreht, dass die Eckpunkte auf den Seiten des äußeren liegen:
{:width="400"}
Wie man leicht sieht (hier aber wirklich!), ist das innere Quadrat halb so groß wie das äußere, also ½*a*². Mit *a* = 10 cm ergeben sich 50 cm².
[^symm]: Aus Symmetriegründen fallen die Mittelpunkte von *ABCD* und *IJKL* zusammen.
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann


