Mathematik zum Schokoladenstreit – Lösung
bearbeitet von@@Gunnar Bittersmann
Wieder eine [Aufgabe von Catriona Shearer](https://twitter.com/Cshearer41/status/1282264739154997248). Sie schreibt dazu: *“I came up with this one a couple of weeks ago, but didn’t ever draw it up properly. Today I found this sketch a margin. I’d completely forgotten how to solve it - it took me quite a while and several false starts! Then one key insight and I could do it in my head.”*{:@en}
[](/images/c136cce4-cfcc-11ea-9634-b42e9947ef30.jpg)
Wir nehmen gleich mal diese Orientierung und legen das Koordinatensystem so, dass *O*(0, 0), *A*(1, 0), *C*(0, 1), *Q*(0, *q*) mit 0 < *q* < 1. Der Mittelpunkt von *QA* ist dann *M*(½, ½*q*).
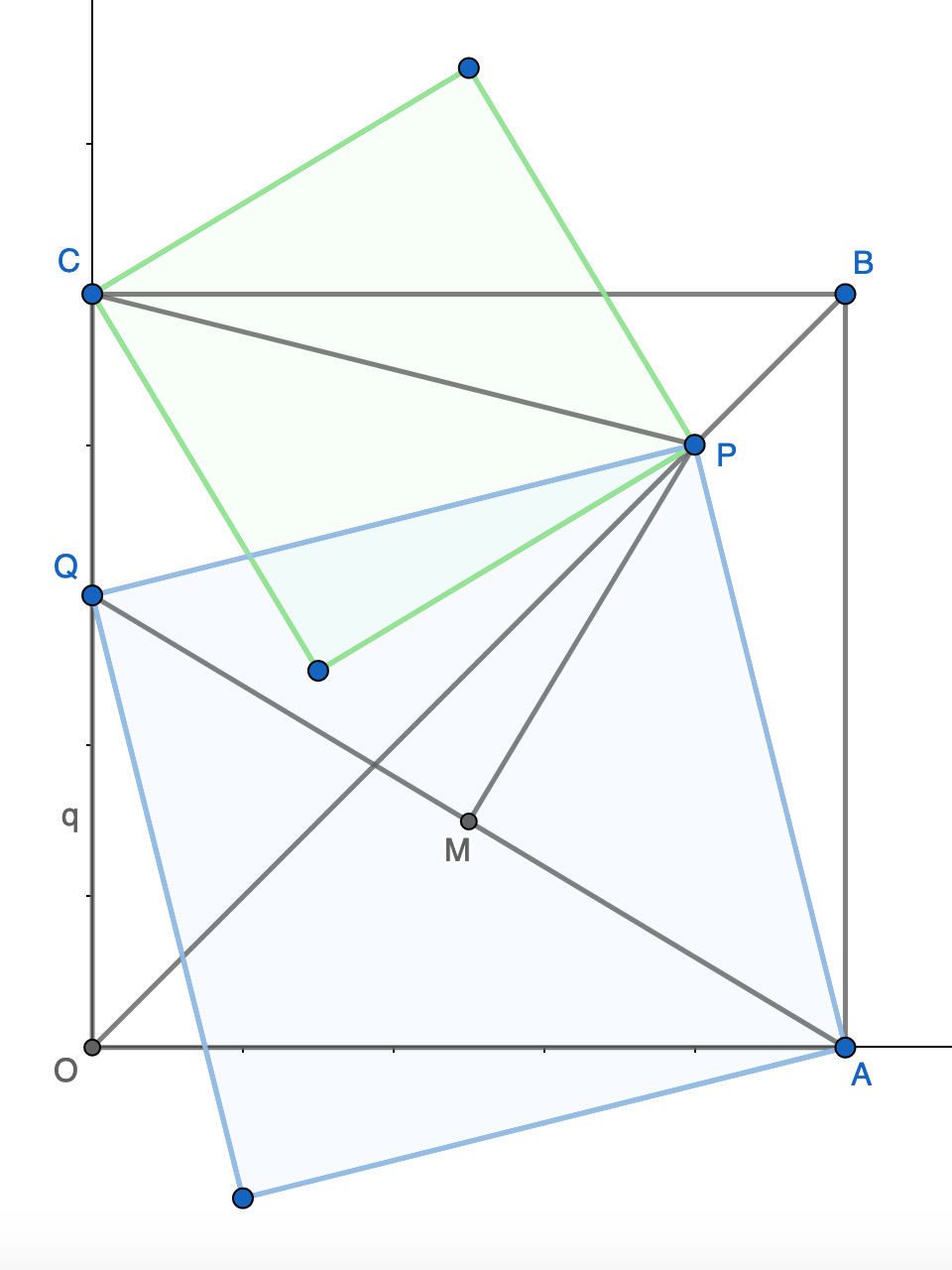
$$\overrightarrow{OP}=\overrightarrow{OQ}+\overrightarrow{QM}+\overrightarrow{MP}=\dbinom{0}{q}+\dbinom{\frac{1}{2}}{-\frac{1}{2}q}+\dbinom{\frac{1}{2}q}{\frac{1}{2}}=\dbinom{\frac{1}{2}q+{\frac{1}{2}}}{\frac{1}{2}q+{\frac{1}{2}}}$$,[^1]
d.h. *P* liegt auf der Geraden *y* = *x*, der Diagonalen von *OABC*.
(Für dies *„key insight“*{:@en} muss man aber nicht die Vektorrechnung bemühen; das lässt sich auch geometrisch zeigen. @Tabellenkalks Herleitung begann mit „Wie man leicht sieht“ – da schrillten bei mir erstmal die Alarmglocken. 🤯 Man kann’s aber [wirklich sehen](https://twitter.com/ChrisWestBass/status/1282606017994469378).)
Aus Symmetriegründen ist *CP* = *AP*, die Diagonale der grünen Quadrats ist so lang wie eine Seite des blauen. Die Seitenlängen der beiden Quadrate verhalten sich wie 1 : √2, die Flächen wie 1 : 2. Die Fläche des blauen Quadrats beträgt also **32**.
[^1]: Dieses LaTeX-Dingens ist ziemlich unbrauchbar. Da geht ja gar nichts mehr, nicht einmal Matritzen.
🖖 Stay hard! Stay hungry! Stay alive! **Stay home!**
{:@en}
--
*“Turn off CSS. If the page makes no sense, fix your markup.”* —fantasai
{:@en}
Mathematik zum Schokoladenstreit – Lösung
bearbeitet von@@Gunnar Bittersmann
Wieder eine [Aufgabe von Catriona Shearer](https://twitter.com/Cshearer41/status/1282264739154997248). Sie schreibt dazu: *“I came up with this one a couple of weeks ago, but didn’t ever draw it up properly. Today I found this sketch a margin. I’d completely forgotten how to solve it - it took me quite a while and several false starts! Then one key insight and I could do it in my head.”*{:@en}
[](/images/c136cce4-cfcc-11ea-9634-b42e9947ef30.jpg)
Wir nehmen gleich mal diese Orientierung und legen das Koordinatensystem so, dass *O*(0, 0), *A*(1, 0), *C*(0, 1), *Q*(0, *q*) mit 0 < *q* < 1. Der Mittelpunkt von *QA* ist dann *M*(½, ½*q*).

$$\overrightarrow{OP}=\overrightarrow{OQ}+\overrightarrow{QM}+\overrightarrow{MP}=\dbinom{0}{q}+\dbinom{\frac{1}{2}}{-\frac{1}{2}q}+\dbinom{\frac{1}{2}q}{\frac{1}{2}}=\dbinom{\frac{1}{2}q+{\frac{1}{2}}}{\frac{1}{2}q+{\frac{1}{2}}}$$,[^1]
d.h. *P* liegt auf der Geraden *y* = *x*, der Diagonalen von *OABC*.
(Für dies *„key insight“*{:@en} muss man aber nicht die Vektorrechnung bemühen; das lässt sich auch geometrisch zeigen. @Tabellenkalks Herleitung begann mit „Wie man leicht sieht“ – da schrillten bei mir erstmal die Alarmglocken. 🤯 Man kann’s aber [wirklich sehen](https://twitter.com/ChrisWestBass/status/1282606017994469378).)
Aus Symmetriegründen ist *CP* = *AP*, die Diagonale der grünen Quadrats ist so lang wie eine Seite des blauen. Die Seitenlängen der beiden Quadrate verhalten sich wie 1 : √2, die Flächen wie 1 : 2. Die Fläche des blauen Quadrats beträgt also 64.
[^1]: Dieses LaTeX-Dingens ist ziemlich unbrauchbar. Da geht ja gar nichts mehr, nicht einmal Matritzen.
🖖 Stay hard! Stay hungry! Stay alive! **Stay home!**
{:@en}
--
*“Turn off CSS. If the page makes no sense, fix your markup.”* —fantasai
{:@en}


