[MATHE] Schnelle Implementierung der Tribonacci-Zahlen

[Wouzhuo]

Hallo,

ich kriege es nicht hin, eine beliebige Zahl der Tribonacci-Folge gut zu implementieren. Ich möchte es nicht rekursiv oder iterativ machen.

Dazu soll folgende Formel dienen...

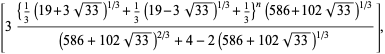
...wobei n (über der dem Term in den geschweiften Klammern) die n-te Tribonacci-Zahl darstellt, wenn man die Folge mit 0 1 1 beginnt.

Ich habe die Formel wie folgt "vereinfacht":

f(n) = 0.336228116994941094225362280443706248543829536991 * 1.839286755214161132551852564653286600424178746097592246778758639404203222047^n

Natürlich stellt die Ausgabe immer nur eine Annährung an die "richtige" Tribonacci-Zahl dar.
Das Problem was ich nun habe ist, dass diese Annährung bis ca n=90 ziemlich genau ist, dann aber sehr schnell ungenau wird.
Bei n=100 unterscheidet sich meine Implementierung von der "richtigen" Fibonacci-Zahl bereits um ~196. Bei n=200 ist es sogar schon eine Differenz von einer Zahl mit über 50 Stellen. Dennoch bin ich mir ziemlich sicher, dass ich eigentlich beim reinen Ausrechnen der Formel keinen Fehler gemacht habe. Auch Rundungsfehler lassen sich bei n=100 wohl ausschließen, da ich mit Datentypen rechne, bei denen während des Potenzierens in einem solch kleinen Bereich erst ab der 1000sten Stelle gerundet wird. Ist also die Formel falsch?