[MATHE] Schnelle Implementierung der Tribonacci-Zahlen
Wouzhuo
- sonstiges
Hallo,
ich kriege es nicht hin, eine beliebige Zahl der Tribonacci-Folge gut zu implementieren. Ich möchte es nicht rekursiv oder iterativ machen.
Dazu soll folgende Formel dienen...
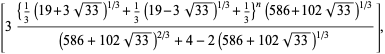
...wobei n (über der dem Term in den geschweiften Klammern) die n-te Tribonacci-Zahl darstellt, wenn man die Folge mit 0 1 1 beginnt.
Ich habe die Formel wie folgt "vereinfacht":
f(n) = 0.336228116994941094225362280443706248543829536991 * 1.839286755214161132551852564653286600424178746097592246778758639404203222047^n
Natürlich stellt die Ausgabe immer nur eine Annährung an die "richtige" Tribonacci-Zahl dar.
Das Problem was ich nun habe ist, dass diese Annährung bis ca n=90 ziemlich genau ist, dann aber sehr schnell ungenau wird.
Bei n=100 unterscheidet sich meine Implementierung von der "richtigen" Fibonacci-Zahl bereits um ~196. Bei n=200 ist es sogar schon eine Differenz von einer Zahl mit über 50 Stellen. Dennoch bin ich mir ziemlich sicher, dass ich eigentlich beim reinen Ausrechnen der Formel keinen Fehler gemacht habe. Auch Rundungsfehler lassen sich bei n=100 wohl ausschließen, da ich mit Datentypen rechne, bei denen während des Potenzierens in einem solch kleinen Bereich erst ab der 1000sten Stelle gerundet wird. Ist also die Formel falsch?
Liebe(r) Wouzhuo,
Tribonacci-Zahl
und ich dachte immer, diese Zahlen nennt man Fibonacci-Zahlen
Liebe Grüße,
Felix Riesterer.
Hi,
Tribonacci-Zahl
und ich dachte immer, diese Zahlen nennt man Fibonacci-Zahlen
Bei den Fibonacci-Zahlen werden immer die vorherigen 2 Zahlen zum neuen Wert aufaddiert (die sind nach Leonardo Fibonacci benannt), bei den Tribonacci-Zahlen werden jeweils die letzten drei (daher das Tri im Namen) Zahlen zum neuen Wert aufaddiert.
cu,
Andreas
Hi,
Natürlich stellt die Ausgabe immer nur eine Annährung an die "richtige" Tribonacci-Zahl dar.
Das Problem was ich nun habe ist, dass diese Annährung bis ca n=90 ziemlich genau ist, dann aber sehr schnell ungenau wird.
Welchen Datentyp verwendest Du denn in Deinem Programm? Bedenke, daß im Computer Zahlen immer in einer endlichen Genauigkeit gespeichert werden (das gilt auch für evtl. vorhandene Zwischenergebnisse).
Schau, ob es bei der von Dir verwendeten Progammiersprache ggf. Datentypen mit höherer Genauigkeit gibt ...
Bei n=100 unterscheidet sich meine Implementierung von der "richtigen" Fibonacci-Zahl bereits um ~196. Bei n=200 ist es sogar schon eine Differenz von einer Zahl mit über 50 Stellen. Dennoch bin ich mir ziemlich sicher, dass ich eigentlich beim reinen Ausrechnen der Formel keinen Fehler gemacht habe. Auch Rundungsfehler lassen sich bei n=100 wohl ausschließen, da ich mit Datentypen rechne, bei denen während des Potenzierens in einem solch kleinen Bereich erst ab der 1000sten Stelle gerundet wird. Ist also die Formel falsch?
Welchen Datentyp verwendest Du denn, der mit 1000 Dezimalstellen (das wären ca. 3322 bits oder 416 bytes) Genauigkeit rechnet?
cu,
Andreas
Hi,
Natürlich stellt die Ausgabe immer nur eine Annährung an die "richtige" Tribonacci-Zahl dar.
Das Problem was ich nun habe ist, dass diese Annährung bis ca n=90 ziemlich genau ist, dann aber sehr schnell ungenau wird.Welchen Datentyp verwendest Du denn in Deinem Programm?
Ich verwende Scheme als Programmiersprache, was dazu führt, dass ich nicht genau weiß, was da intern passiert. Tatsache ist aber, dass alle rationalen _ohne_ Datenverlust (d.h in Form eines Bruchs) gespeichert werden. Egal wie groß Zähler oder Nenner werden. Falls die Zahlen nicht als Bruch darstellbar sind, werden sie auf 1000 Stellen nach dem Komma kaufmännisch gerundet.
Bedenke, daß im Computer Zahlen immer in einer endlichen Genauigkeit gespeichert werden (das gilt auch für evtl. vorhandene Zwischenergebnisse).
Schau, ob es bei der von Dir verwendeten Progammiersprache ggf. Datentypen mit höherer Genauigkeit gibt ...
Daran kann der Fehler nicht liegen. Selbst wenn ich auf z.B. nur 20 Stellen runden lasse, ändert sich die Differenz (die ja bei n=200 bereits sehr falsch ist) erst bei der 10ten Nachkommastelle. Scheint also irrelevant zu sein.
Ich verwende Scheme als Programmiersprache, was dazu führt, dass ich nicht genau weiß, was da intern passiert.
Ich bin zu unbedarft in Scheme, um da mit Sicherheit sprechen zu können. Allerdings definiert die Spezifikation von Scheme, dass Scheme-Implementationen Integer- und rationale Zahlen auch in einer „Exakten Form“ unterstützen müssen. Dazu gibt es das Prefix #e, um exakte Zahlen repräsentieren zu können, die Funktion (exact? z), um eine Zahl auf Exaktheit überprüfen zu können und bei exakten Argumenten sind viele arithmetische Funktionionen verpflichtet, auch exakt zu arbeiten. Vielleicht gibt es bei konsequenter Nutzung der Exaktheit unterschiedliche Ergebnisse?
Spiel doch mal mit der Genauigkeit deiner Zahl 1,8...
Wie ist der Unterschied wenn du die hinten verkürzt oder verlängerst? Vielleicht ist sie einfach noch zu kurz um bei 200 als Exponent was brauchbares zu liefern?
Wobei das jetzt nur so ne Idee ist, ohne mathematischen Hintergrund, ob eine Änderung an so einer kleinen Stelle bei "hoch 200" wirklich so viel ausmachen kann.
Spiel doch mal mit der Genauigkeit deiner Zahl 1,8...
Wie ist der Unterschied wenn du die hinten verkürzt oder verlängerst? Vielleicht ist sie einfach noch zu kurz um bei 200 als Exponent was brauchbares zu liefern?
Nee, leider nicht... ob ich 1000 Nachkommastellen oder nur 10 benutze, macht im Endergebnis lediglich einen Unterschied bei der 20 Nachkommastelle. Da muss irgendetwas anderes falsch sein.
Wobei das jetzt nur so ne Idee ist, ohne mathematischen Hintergrund, ob eine Änderung an so einer kleinen Stelle bei "hoch 200" wirklich so viel ausmachen kann.
Tja, woran könnte es sonst liegen?
Bei den _Fi_bonacci-Zahlen, klappt es übrigens ohne Probleme.