Mathematik zum Wochenende - Auflösung Teil 3

[Gunnar Bittersmann]

@@Matthias Apsel

Alternativ lässt sich noch eine weitere Hilfslinie hinzufügen, dann wird die Argumentation kürzer:

Ich glaube, ich komme mit weniger Hilflinien und noch kürzerer Argumentation aus:

O.B.d.A. sei AC ≥ BC. Bezeichnung der Punkte siehe Skizze:^[1]

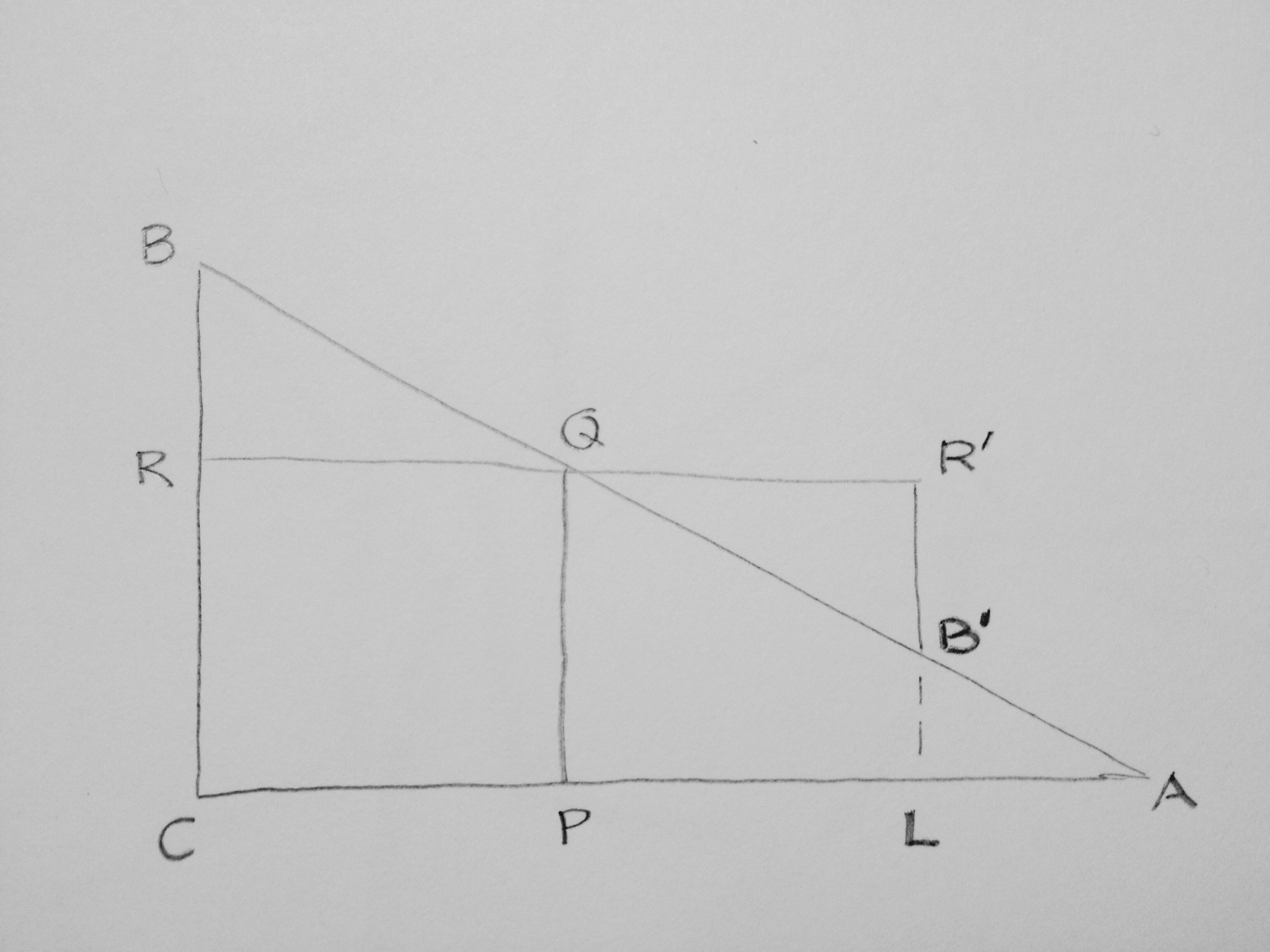
Das Dreieck QBR wird an Q gespiegelt (d.h. um 180° um Q gedreht). Für AC > BC liegt L zwischen P und A; für AC = BC fällt L mit A zusammen. Die Quadrate CPQR und PLRʹQ sind flächengleich.

Die Restfläche des Dreiecks ABC ohne das Quadrat CPQR ist flächengleich dem Quadrat PLRʹQ plus (für AC > BC) dem Dreieck LABʹ; somit mindestens so groß wie das Quadrat CPQR, d.h. das Quadrat CPQR ist höchstens halb so groß wie das Dreieck ABC.

LLAP 🖖

---

1. Nicht barrierefrei, ich weiß. Grmpf. ↩︎