nicht angemeldet
Gunnar Bittersmann
encoder
MudGuard
Matthias Apsel
Gunnar Bittersmann
Tabellenkalk
Rolf b
Tabellenkalk
Gunnar Bittersmann
Rolf b
Tabellenkalk
Rolf b
Tabellenkalk
Bin kürzlich auf dieses nette Rätsel gestoßen: reguläres Achteck. Bestimme auf einfachste Weise das Verhältnis der blauen Trapezfläche zur orangenen Dreiecksfläche!
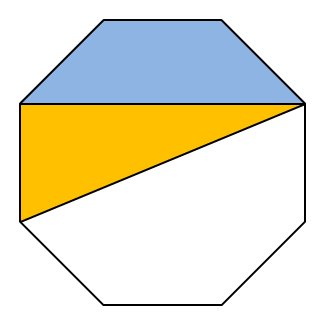
LLAP 🖖
Hallo
Was heißt "einfachste Weise"?
Eine möglichst einfache Erklärung ohne Berechnungen?
Möglichst wenige Berechnungen?
Möglichst einfache Rechenoperationen?
Und welche Grundlagen dürfen als gegeben verwendet werden?
Aus dem Bauch raus würde ich einfach beide Flächen verdoppeln und damit zu Rechtecken machen, deren Flächen einfach berechnet und verglichen werden können um das Verhältnis zu erhalten.
Gruss
MrMurphy
Nach Augenmaß sind die beiden Flächen gleich groß. Also müssten sie dasselbe Gewicht haben.
Auf Karton gedruckt, ausgeschnitten ... Mist, meine Briefwaage und die Küchenwaage rühren sich nicht. Ich forsche weiter ...
Hi,
Nach Augenmaß sind die beiden Flächen gleich groß. Also müssten sie dasselbe Gewicht haben.
Mal abgesehen davon, daß eine Fläche kein Gewicht hat: wenn ich richtig gerechnet habe, liegt Dein Augenmaß um knapp 21% daneben.
Auf Karton gedruckt, ausgeschnitten ... Mist, meine Briefwaage und die Küchenwaage rühren sich nicht.
Nimm eine Bleiplatte ;-)
cu,
Andreas a/k/a MudGuard
Hallo
Flächen haben kein Gewicht, Körper hingegen schon. Gesucht ist ein Verhältnis und dazu können beide Seiten erweitert werden, auch in der dritten Dimension.
Ich finde den praktischen Ansatz von Linuchs spannend. Ich habe mal mit meinem alten Holzspielzeugkasten ein regelmäßiges Achteck nachgebaut und in einer Balkenwaage (die Lösung soll ja möglichst einfach sein) nachgewogen.
Gruss
MrMurphy
Flächen haben kein Gewicht, Körper hingegen schon.
So isses. Was wäre das andere Geschlecht ohne Körper? Richtig: Plankton!
(Dank der grieschichen Philatelie)
Mal abgesehen davon, daß eine Fläche kein Gewicht hat: …
Natürlich nicht. Aber die Druckfarbe, die ich aufgebracht habe 😉 - gilt das? Nun komm nicht damit, dass Blau schwerer ist als Grün.
Uups nicht Grün, sondern Gelb. Der blaue Karton scheint durch.
Linuchs
Hallo,
Auf Karton gedruckt, ausgeschnitten ... Mist, meine Briefwaage und die Küchenwaage rühren sich nicht. Ich forsche weiter ...
versuch es mal mit 20er Rauspund.
Gruß
Jürgen
Was macht man wenn man eine Lösung zu haben glaubt?
Hi,
Was macht man wenn man eine Lösung zu haben glaubt?
Ich hab, um's nicht zu verraten, per persönlicher Nachricht an Gunnar geschickt.
cu,
Andreas a/k/a MudGuard
Hallo MudGuard,
Ich hab, um's nicht zu verraten, per persönlicher Nachricht an Gunnar geschickt.
Und dabei den Betreff vergessen. Mit dem Button unterm Beitrag wär es nicht passiert 😂
Bis demnächst
Matthias
Hi,
Ich hab, um's nicht zu verraten, per persönlicher Nachricht an Gunnar geschickt.
Und dabei den Betreff vergessen. Mit dem Button unterm Beitrag wär es nicht passiert 😂
Aber dann wäre der Fehler mit der doppelten Fehlermeldung und ddem fehlenden required immer noch ungefixt 😉
cu,
Andreas a/k/a MudGuard
Mit dem Button unterm Beitrag wär es nicht passiert 😂
Ach das soll "neue Mail" bedeuten. "Mail an den Autor" hätte ich eher verstanden.
Na egal. Hab ich eben manüll eine Mail an ihn verschickt.
Rolf
Hallo Rolf b,
Ach das soll "neue Mail" bedeuten. "Mail an den Autor" hätte ich eher verstanden.
Ist „Autor kontaktieren“ auch ok? 😉
Bis demnächst
Matthias
@@encoder
Was macht man wenn man eine Lösung zu haben glaubt?
Man wiegt sie. Es ist ja die leichteste Lösung gefragt. 😉
Tip: Wenn die Lösung oder der Weg dahin eine Wurzel enthält, dann knobelt man weiter.
LLAP 🖖
Hallo,
Man wiegt sie. Es ist ja die leichteste Lösung gefragt. 😉
Hm, im OP ist noch von der einfachsten Lösung die Rede, also nix mit Wiegen und auch nix mit Flächen zweifach nehmen...
Gruß
Kalk
(...) auch nix mit Flächen zweifach nehmen...
Aber halbieren darf ich?
Hallo,
Bestimme auf einfachste Weise das Verhältnis der blauen Trapezfläche zur orangenen Dreiecksfläche!
Ich glaube, die zwei haben ein sehr enges Verhältnis miteinander‼️
Gruß
Kalk
@@Tabellenkalk
Ich glaube, die zwei haben ein sehr enges Verhältnis miteinander‼️
Man könnte glatt sagen: sie sind ein Herz und eine Seele.
LLAP 🖖
Auf einfache Art und Weise versuche ich mir vorzustellen, wie das 8eck entstanden ist: Infolge Übereinanderlegung 2er Quadrate wobei eins von denen um 45° gedreht wurde.
Aus dieser Situation heraus hätten orange und blaue Fläche dieselbe Größe wenn sie nicht beschnitten wären. Aber sie wurden eben beschnitten wie folgt:
Also ist die blaue Fläche größer, über einen gemeinsamen Nenner gerechnet im Verhältnis 3:2
Tooooooooooooooor!!!
Hallo
Ich dachte so was nennt man Eigentor.
Gruss
MrMurphy
[..] und ich dachte, ich bekommen einen Ehrenkranz weil ich die Lösung mit Hammer und Zirkel gefunden habe.
Freundschaft 😉
@@pl
[..] und ich dachte, ich bekommen einen Ehrenkranz weil ich die Lösung mit Hammer und Zirkel gefunden habe.
Gefragt war nicht nur die einfachste Lösung, sondern auch die richtigste.
Hätte ich vielleicht eingangs dazuschreiben sollen.
Freundschaft 😉
Immer bereit
LLAP 🖖
Hallo,
Freundschaft 😉
Immer bereit
oder auch: Druschba! - Allzeit breit!
Gruß
Kalk
Hallo Tabellenkalk,
oder auch: Druschba! - Allzeit breit!
Дружба!
Bis demnächst
Matthias
@@Matthias Apsel
Freundschaft 😉
Immer bereit
oder auch: Druschba! - Allzeit breit!
Дружба!
Всегда мы вместе, ГДР и Советский Союз. ♫
LLAP 🖖
@@Gunnar Bittersmann
Falls es wen interessiert: Ich kam auf diese Lösung:
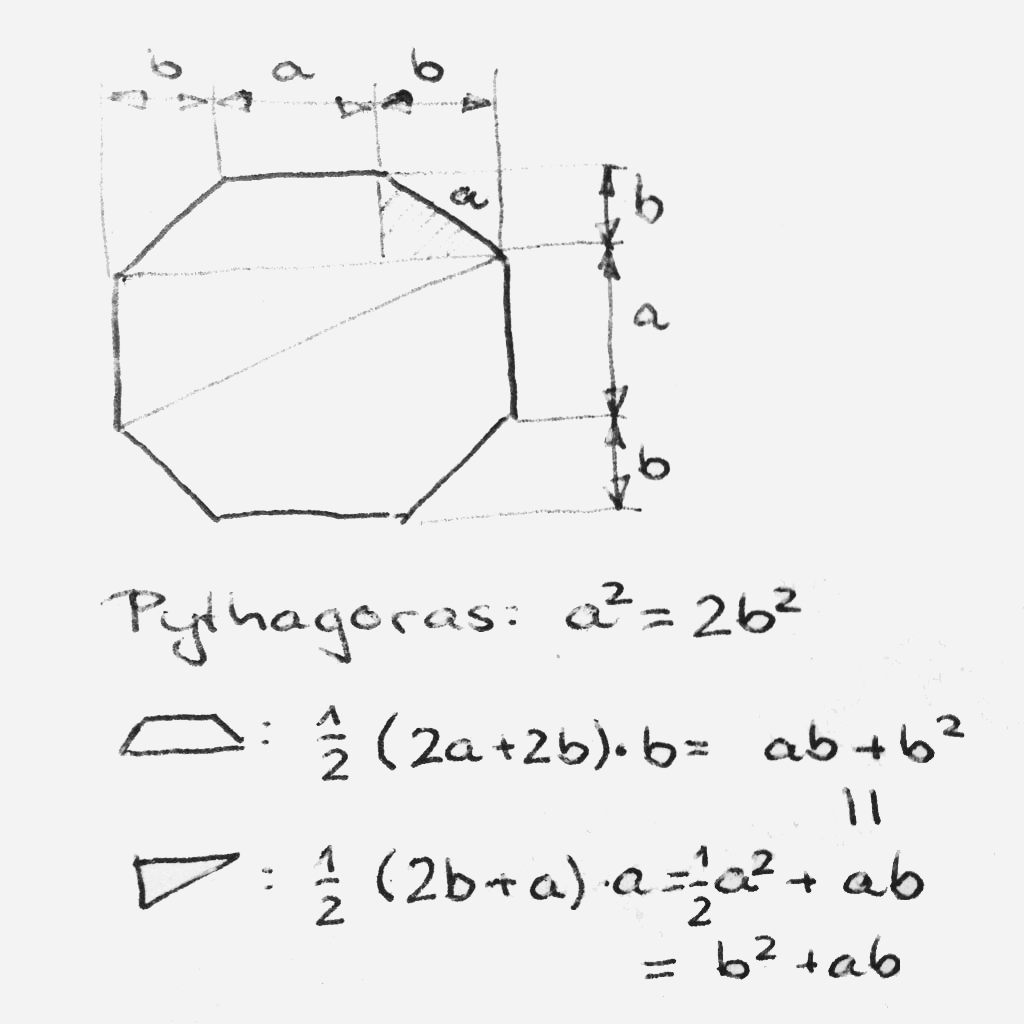
Wie ich versprach: ohne Wurzeln. Aber immer noch mit Rechnerei.
Geht aber einfacher: mit Hilfslinien Flächen zerteilen und vergleichen. Die Musterlösung von @Five_Triangles:
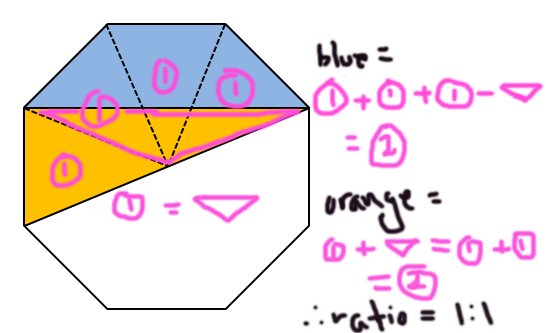
@Rolf b hatte das auch in etwa so.
Eine andere Variante kam von @encoder und @ottogal: Hilflinien nicht zu den Eckpunkten, sondern Richtung Seitenmitten:
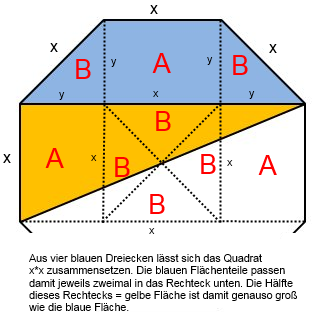
LLAP 🖖
Moin,
Hm... ich hab nur das Verhältnis der Höhen der einzelnen zu bildenden Streifen (und damit der Flächenverhältnisse) gebildet und bin dann so zum Ergebnis gekommen. Hab bissl hin und her überlegt ohne groß zu rechnen. Einzig das Verhältnis war hier entscheidend.
Gruß Bobby
Moin,
OK... eine Wurzel hab ich gezogen... Wurzel aus 2 = 1,41
Gruß Bobby
Und wenn ich nicht irre, auch approximiert - deine 7 ist doch eigentlich eine 7,071 ($$10\cdot\frac{1}{2}\sqrt 2$$), oder?
Und wie Du Dein $$ \frac{1}{10}$$ motivierst, finde ich auch nicht offensichtlich. Bitte erhelle meine Blindheit.
Rolf
Moin,
Und wenn ich nicht irre, auch approximiert - deine 7 ist doch eigentlich eine 7,071 ($$10\cdot\frac{1}{2}\sqrt 2$$), oder?
Na selbstverständlich gerundet. Das Verhältnis der beiden Flächen ist ja auch nicht GENAU 1:1
Und wie Du Dein $$ \frac{1}{10}$$ motivierst, finde ich auch nicht offensichtlich. Bitte erhelle meine Blindheit.
Der oberen Streifen hat 7/10 Fläche. Darüber sind wir uns hoffentlich einig.
Die Außenkanten der fehlenden 3-Ecke haben auch die Länge von 7 (ist ja alles regelmäßig) korrekt? Somit wäre die Außenkante des erweiterten Quadrats (also die Außenkanten inkl. der 3 Ecke) 10+2*7. Richtig?
Also haben wir eine Fläche des mittleren Quadrats von 24*10 (natürlich gerundet) = 240. Die 240 sind 10/10
Nun kann ich den Flächenanteil der 3-Ecke berechnen (7*7)/2 (weil Außenkannten ja 7) = 24,5 Also Rund 1/10 der Gesamtfläche des mittleren Rechteckes.
Nun bekomm ich auch den Flächeninhalt der blauen Fläche und der gelben Fläche heraus
blau: unterteilt in 1 Quadrat 7 * 10 + 2 Dreiecke wie oben berechnet (24,5) => 7 * 10 + 2 * 24,5 = 119
gelb ist die Hälfte der 10/10-Fläche also 240 / 2 = 120
blau: 119 gelb: 120 macht RUND ein Ergebnis von 1:1
erleuchtet? Ich habe die Außenkanten des Achtecks also einfach mal als 10 angenommen. So mußte ich nur die Außenkanten der weg geschnittenen 3-Ecke berechnen (mit der angesprochenen Wurzel). Alles andere hat sich selbst ergeben.
Gruß Bobby
Hallo,
Na selbstverständlich gerundet. Das Verhältnis der beiden Flächen ist ja auch nicht GENAU 1:1
Hast du Gunnars Lösungssammlung gelesen?
Gruß
Kalk
Ok, jetzt habe ich verstanden wie du vorgegangen bist. Und es erinnert mich an die Ingenieure, die vor dem Taschenrechnerzeitalter ausgebildet wurden.
Ich: "Wieviel ist 3 mal 4?"
Ing: (raschel - ssst - sssst) "11,99"
Ich: "Echt jetzt?"
Ing: "Na gut, ein halbes Promille ist immer drin!"
Rolf
Edit: Keine Ahnung warum er das Bild nicht mehr inline anzeigt, sobald man einmal das Bild-Tag angefasst hat.
Hallo Rolf,
Edit: Keine Ahnung warum er das Bild nicht mehr inline anzeigt, sobald man einmal das Bild-Tag angefasst hat.
Die Syntax für Inline-Bilder ist  😉 Das Ausrufungszeichen ist relevant 😀
LG,
CK
Hallo,
Geht aber einfacher: mit Hilfslinien Flächen zerteilen und vergleichen. Die Musterlösung von @Five_Triangles:
Hier fehlen mir zwei Dinge: die eingekreiste "2" ist nicht in der Zeichnung zu finden, und für die Behauptung "1" = "Dreieck" wäre vielleicht noch eine kleine Hilfslinie vom Mittelpunkt nach oben erhellend gewesen.
Gruß
Kalk
JürgenB