mySQL: Nachbarorte finden

[Linuchs]

Moin,

der Berechnung von Entfernungen liegt eine - für mich - komplizierte Formel zugrunde.

Bisher habe ich in einem ersten SELECT die geo_breite und geo_laenge des zentralen Ortes aus der DB geholt und mit PHP umgesetzt:

$rad_lat1    = deg2rad( $row_zentrum['geo_breite'] );
$rad_lon1    = deg2rad( $row_zentrum['geo_laenge'] );

Die 10 Nachbarorte dann mit einem zweiten SELECT geholt:

SELECT
...
,ROUND( 6366.19773095 * ACOS( SIN(".$rad_lat1.") *SIN(RADIANS(ort1.geo_breite)) +COS(".$rad_lat1.") *COS(RADIANS(ort1.geo_breite)) *COS(RADIANS(ort1.geo_laenge) -".$rad_lon1." ))) dist_km
...
GROUP BY  ...
ORDER BY dist_km
LIMIT 0,10

Nun brauche ich für Ajax-Vorschlagswerte ein schnelleres Verfahren. Da mySQL auch RADIANS() kennt, möchte ich das künftig mit nur einem SELECT erledigen.

Der zentrale Ort ist im SQL ort1, die gesuchten Nachbarn sind ort2. Nun müsste die Formel in etwa so aussehen:

,ROUND( 6366.19773095 * ACOS( SIN(RADIANS(ort1.geo_breite)) *SIN(RADIANS(ort1.geo_breite)) +COS(RADIANS(ort1.geo_breite)) *COS(RADIANS(ort1.geo_breite)) *COS(RADIANS(ort1.geo_laenge) -RADIANS(ort1.geo_laenge) ))) dist_km

Ich werde das Gefühl nicht los, dass das Konstrukt ACOS( SIN(RADIANS(ort1.geo_breite)) doppelt oder dreifach gemoppelt ist.

Ich habe für ort1 geo_laenge und geo_breite, möchte die Orte ort2 im Umkreis von 20 km finden, die auch geo_laenge und geo_breite haben. Geht das nicht einfacher?

Linuchs

[Rolf b]

Google findet relativ zügig diese Näherungsformel. Hilft dir die?

[Linuchs]

Das Beschreiben eines Problems ist ja schon der erste Schritt zur Lösung.

Ich denke, ich berechne nicht umständlich einen Kreis, sondern setze den zentralen Ort gedanklich in ein Quadrat mit vier Eckpunkten.

Ist nicht ganz korrekt, aber eines schnellen DB_Zugriffs zuträglich.

So hatte ich es mal vor Urzeiten, als ich die Kreisformel noch nicht kannte.

Linuchs

[dedlfix]

Tach!

Ich habe für ort1 geo_laenge und geo_breite, möchte die Orte ort2 im Umkreis von 20 km finden, die auch geo_laenge und geo_breite haben. Geht das nicht einfacher?

Das Thema ist nicht neu und steht schon oft im hiesigen Archiv. Die einfachste Weise ist, Quadrate zu nehmen und die Krümmung der Erdoberfläche zu vernachlässigen, wenn es sich um einen überschaubar kleinen Bereich handelt.

dedlfix.

[TS]

Hallo und guten Tag,

wie man hier jetzt ein Quote macht, weiß ich leider nicht....

<quote> Das Thema ist nicht neu und steht schon oft im hiesigen Archiv. Die einfachste Weise ist, Quadrate zu nehmen und die Krümmung der Erdoberfläche zu vernachlässigen, wenn es sich um einen überschaubar kleinen Bereich handelt. </quote>

... und wenn man meine uralten Posts dazu auch lesen würde, dann könnte nan das sogar fertig machen:

Einfach arbeiten, wie ein Computer und eben nicht, wie ein Mathematiker, also iterativ! Im ersten Schritt (select) die oben genannten "Quadrate" holen (sind sie auf einer Kugel ja auch nicht), und dann diese Zwischenergebnismenge mit der Formel für sphärische Geometrie filtern. Das kann man auch im DBMS machen oder aber in der API.

Und wer diese Aufgabe öfter zu lösen hat, schreibt sich für die zweistufige Lösung eine Funktion für MySQL.

Liebe Grüße
TS

[Christian Kruse]

Hallo TS,

wie man hier jetzt ein Quote macht, weiß ich leider nicht....

Link in der MOTD beachten.

LG,
CK

[Regina Schaukrug]

SELECT
...
,ROUND( 6366.19773095 * ACOS( SIN(".$rad_lat1.") *SIN(RADIANS(ort1.geo_breite)) +COS(".$rad_lat1.") *COS(RADIANS(ort1.geo_breite)) *COS(RADIANS(ort1.geo_laenge) -".$rad_lon1." ))) dist_km
...
GROUP BY  ...
ORDER BY dist_km
LIMIT 0,10

Das Problem ist doch alt: Jede Berechnung mit Werten aus den Tabellen in der WHERE-Clausel führt zu einem FULL-TABLE-SCAN und ist also langsam. Schreib EXPLAIN vor das SELECT und Du siehst es.

Suche Orte mit maximaler und minimaler Länge und Breite, dann bleiben die Indizes nutzbar. Kreisberechnung dann nur für diese Auswahl (entweder temporäre Tabelle oder aber als Iteration über den Ergebnis-Array in der Programmiersprache, welche die Datenbank befragt.)

[TS]

Hallo und guten Tag Linuchs,

deine Frage hat mich doch nochmal zurückversetzt in meine Überlegungen von 2000. Da waren die leider nicht weiter diskutiert worden.

Aufgabenstellung war, auf der Kugeloberfläche (Erde) mittels Datenbank eine Treffer(ober)menge für gesuchte Nachbarn zu finden unter Benutzung von Koordianten des umschließenden (quasi-)Rechteckes. Dabei sollen die Strecken in Nord-Süd-Richtung und die in Ost-West-Richtung möglichst gewahrt bleiben.

Die Strecken in Nord-Süd-Richtung sind direkt Proportional zum Umfangssektor auf dem Lägengrad.
Die Strecken in Ost-West-Richtung sind aber abhängig vom Breitengrad, auf dem sie absolviert werden müssen.

Wie könnte man nun ein (linares) Koordinatensytem für erste Näherungen aufbauen, in dem die Strecken (auf der Kugeloberfläche) in beide Richtungen berücksichtigt werden?

Ich bekomme das leider nicht hin, das zu zeichnen. Vieleicht gibt's ja jemanden mit grafischen Ambitionen, der das mal veranschaulichen könnte?

Jedenfalls wird der zulässige Ost-West Wertebereich immer geringer, je weiter man vom Äquator entfernt ist. Gibt es da schon ein etabliertes Rechensystem?

Liebe Grüße
TS

[JürgenB]

Hallo,

mit folgender Funktion berechne ich Eckkoordinaten, um eine Google Maps Karte zu skalieren:

JB.bounds = function(center_lat,center_lon,radius) {
	var d = radius/6378.137;
	var fak = Math.PI/180;
	var lat = center_lat * fak;
	var lon = center_lon * fak;
	var sind = Math.sin(d);
	var cosd = Math.cos(d);
	var sinlat = Math.sin(lat);
	var coslat = Math.cos(lat);
	var latmin = (Math.asin(sinlat*cosd - coslat*sind))/fak;
	var latmax = (Math.asin(sinlat*cosd + coslat*sind))/fak;
	var lonmin = (lon - Math.asin(sind/coslat))/fak;
	var lonmax = (lon + Math.asin(sind/coslat))/fak;
	return {latmin:latmin,latmax:latmax,lonmin:lonmin,lonmax:lonmax};
} // JB.bounds

center_lat und center_lon, sind die Koordinaten des Mittelpunktes in Grad, radius der Radius in km. Mehr dazu siehe http://de.wikipedia.org/wiki/Wegpunkt-Projektion. Hier findest du auch eine Näherungsformel für kurze Entfernungen.

Gruß
Jürgen

[JürgenB]

Hallo Tom,

das hatten wir doch schon mal: https://forum.selfhtml.org/self/2016/apr/23/geodaten/1665852#m1665852

Gruß
Jürgen

[Linuchs]

Hallo TS,

Wie könnte man nun ein (linares) Koordinatensytem für erste Näherungen aufbauen, in dem die Strecken (auf der Kugeloberfläche) in beide Richtungen berücksichtigt werden?

Habe ich auch schon überlegt. Man müsste auf dem Globus mit der Idee der gleichen Abstände zwischen Breitengraden sogenannte Self-Grade (von selfHTML) rot einzeichnen.

Jeder Punkt des Globusses liegt nun auf einer Kreuzung eines bestimmten Breitengrades mit einem bestimmten Self-Grad, die Abstände der beiden Koordinaten sind überall konstant.

Genauer: Breiten- und Selfkreise haben je zwei Kreuzungspunkte oder genau eine Tangentialberührung. In der Draufsicht ist oben rechts zwischen Selfkreis (rot) und Breitenkreis (grün) so ein Tangentialpunkt. Diese beiden Kreise berühren sich, kreuzen sich aber nicht:

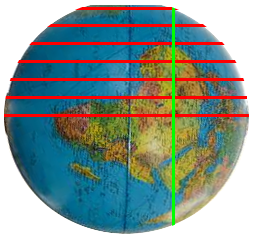
Frage an Mathematiker: Wie kann man den Selfkreis eines Punktes auf dem Globus errechnen?

[MudGuard]

Hi,

Bisher habe ich in einem ersten SELECT die geo_breite und geo_laenge des zentralen Ortes aus der DB geholt und mit PHP umgesetzt:

Dir ist bewußt, daß das nur die Luftlinie berücksichtigt?

Unter Umständen ist die zu fahrende Strecke von A nach B aber deutlich länger als die Luftlinie.

Je nach Zweck der Nachbarortssuche kann das relevant sein oder auch nicht.

Beispiele:

Luftlinie von Rosroe, Co. Galway, Ireland nach Doovilra, Co. Mayo, Ireland sind etwa 2km. Mit dem Auto ist man aber ca. 52km unterwegs, weil man um einen Fjord und ein paar Hügel außenrum fahren muß.

Oder Steckborn (CH) -> Gaienhofen (DE), Luftlinie 2km, Fahrstrecke 20km, weil der Bodensee dazwischen ist.

cu,
Andreas a/k/a MudGuard