Mathematik zum Sonntagnachmittagskaffee
- mathematik
Hallo in die Runde,
meine Mutter (die heute 95 Jahre alt geworden wäre) pflegte ihre Freundinnen manchmal zum Kaffeklatsch einzuladen. Vor dem Aufteilen der Torte markierte sie die Schnittlinien mit einem sogen. "Tortenteiler" (mal nach Bildern Ixquicken...)
Nun hörte sie immer mal wieder den Spruch "Für mich nur ein kleines Stück!", was sie auf die Idee brachte, den Tortenteiler leicht exzentrisch aufzudrücken - siehe die Zeichnung.
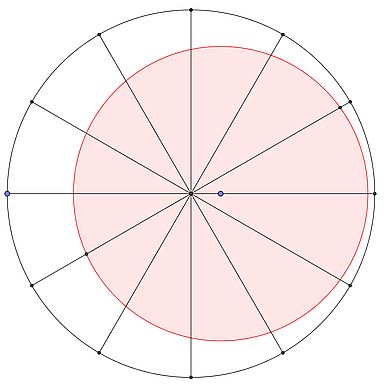
Angenommen, der Abstand d der Kreiszentren ist 20% des Kuchenradius. Zu berechnen ist, wie groß das größte und das kleinste Tortenstück sind, in % der gesamten Torte. (Bei symmetrischer Aufteilung wäre natürlich jedes Stück 1/12 = 8,33% groß.)
Schön wären freilich Formeln mit d als Variable...
Und dann gibts ja noch die anderen Stücke... Aber da müsste man sich erstmal mit einem Stück Torte stärken!
Viel Spaß
ottogal
Hey,
Soll der Punkt so verschoben sein wie auf der Skizze oder bei dem Halben Winkel des Kreissegments?
Wie es in der skizze ist hat man 2 größte und kleinste Kuchenstücke.
Gruß
Jo
Hallo ottogal,
Angenommen, der Abstand d der Kreiszentren ist 20% des Kuchenradius. Zu berechnen ist, wie groß das größte und das kleinste Tortenstück sind, in % der gesamten Torte. (Bei symmetrischer Aufteilung wäre natürlich jedes Stück 1/12 = 8,33% groß.)
Wenn der Tortenteiler wie in deiner Zeichnung aufgesetzt wird, dann gibt es jeweils zwei größte und kleinste Tortenstückchen.
Schön wären freilich Formeln mit d als Variable...
Und für den Gunnar noch mit β als Drehwinkel …
Viel Spaß
Danke.
Und nicht zu früh verraten. Wegen des Spaßes.
Bis demnächst
Matthias
@@Matthias Apsel
Und für den Gunnar noch mit β als Drehwinkel …
Bin gerade in anderen Winkeln der Welt unterwegs.
Ich hätte euch ja gern wieder ein Bilderrätsel „Wo bin ich?“ gestellt, aber der Bilderupload ist immer noch kapautt. :-(
Kann sich dieses Bugs mal jemand annehmen?
LLAP 🖖
Hallo Gunnar Bittersmann,
Kann sich dieses Bugs mal jemand annehmen?
Falls es an der Dateigröße liegt, würde ich sagen, es ist kein Bug. Die maximale Bilddateigröße lässt sich einstellen, was schlägst du vor?
Bis demnächst
Matthias
@@Matthias Apsel
Falls es an der Dateigröße liegt, würde ich sagen, es ist kein Bug.
Schlechte UX ist ein Bug.
Die maximale Bilddateigröße lässt sich einstellen, was schlägst du vor?
Das bereits Gesagte. Und sinnvolle Maßnahmen gegen DDoS-Attacken ergreifen, nicht irgendwelche.
Vielleicht kann man den Upload auch mit der Registrierung verknüpfen und registrierten Nutzern keine Beschränkung auferlegen.
LLAP 🖖
Hallo Gunnar Bittersmann,
Schnell und schmutzig:
Versende das Bild an irgendjemanden per WhatsApp, Threema oder einem ähnlichen Messenger. Lade dieses Bild hoch.
Bis demnächst
Matthias
@@Matthias Apsel
Schnell und schmutzig:
Ich bin an einer sauberen Lösung interessiert. Gern auch schnell.
Versende das Bild an irgendjemanden per WhatsApp …
Er hat „WhatsApp“ gesagt! 😱 Nutzer-Ausspionieren der übelsten Sorte.
LLAP 🖖
@@Matthias Apsel
Schnell und schmutzig:
Versende das Bild an irgendjemanden per WhatsApp, Threema oder einem ähnlichen Messenger. Lade dieses Bild hoch.
Bin ich im falschen Film? Hab ich aber mal gemacht. Wo bin ich?

Da mein letztes Bilderrätsel zu schwer war, dache ich, ich mach es euch mal ein bisschen einfacher. ;-)
LLAP 🖖
Hallo Gunnar Bittersmann,
Bin ich im falschen Film? Hab ich aber mal gemacht. Wo bin ich?
Da war ich auch schon.
Bis demnächst
Matthias
Hallo Gunnar,
Bin ich im falschen Film? Hab ich aber mal gemacht. Wo bin ich?
Da mein letztes Bilderrätsel zu schwer war, dache ich, ich mach es euch mal ein bisschen einfacher. ;-)
Welcher von den Vieren bist Du denn? ;-P
Grüße
TS
@@TS
Welcher von den Vieren bist Du denn? ;-P
Da ich was mit dem Internet zu tun habe, ja wohl die Katze. 😼
LLAP 🖖
Hallo und guten Tag,
Welcher von den Vieren bist Du denn? ;-P
Da ich was mit dem Internet zu tun habe, ja wohl die Katze. 😼
Hätte ich eigentlich auch selber drauf kommen können ;-)
Grüße
TS
Hallo und guten Morgen,
Vielleicht kann man den Upload auch mit der Registrierung verknüpfen und registrierten Nutzern keine Beschränkung auferlegen.
Keine Beschränkung ist nur schwer möglich, da das gesamte System auf den Upload vorbereitet sein muss.
Genauer kann ich das jetzt nur für PHP spezifizieren:
Siehe Wiki
Grüße
TS
Es ist so gemeint wie in der Zeichnung. Klar, das größte und das kleinste Stück kommen jeweils zweimal vor.
Hallo in die Runde,
meine Mutter (die heute 95 Jahre alt geworden wäre) pflegte ihre Freundinnen manchmal zum Kaffeklatsch einzuladen. Vor dem Aufteilen der Torte markierte sie die Schnittlinien mit einem sogen. "Tortenteiler" (mal nach Bildern Ixquicken...)
Mit einem echten Tortenteiler sind die Stücken alle gleichgroß, egal ob der exzentrisch reingedrückt wird oder mittig. Der Verschnitt lässt sich über den Durchmesser ausrechnen.
PS: Bei uns gabs heute Rolle -- Linear mit dem Messer geschnitten ;)
Hallo pl,
Mit einem echten Tortenteiler sind die Stücken alle gleichgroß, egal ob der exzentrisch reingedrückt wird oder mittig.
Mal mal auf.
Bis demnächst
Matthias
Hallo und guten Abend,
da gibt's 'was im Netz:
Sehnenberechnun
Der Rest sind Dreiecke mit einem gleichen spitzen Winkel. Aber die Langseiten jedes Dreiecks sind unterschiedlich lang. folglich sind auch die beiden Winkel an der Sehne unterschiedlich...
Grüße
TS
Na, keine/r hier mit Lust auf Torte?
Hallo und guten Abend,
Na, keine/r hier mit Lust auf Torte?
Ich habe das mal an die Gesellenschüler im Bildungswerk weitergegeben, aber die interessieren sich eher für Downloadraten und Likes.
Liebe Grüße
TS
Hallo TS,
Ich habe das mal an die Gesellenschüler im Bildungswerk weitergegeben, aber die interessieren sich eher für Downloadraten und Likes.
Nun ja, die Berechnung der Größen der Tortenstücke ist mit den Mitteln der Integralrechnung kein Problem. Ich denke, das können Gesellenschüler nicht, weil sie das in der Schule niemals hatten.
Ohne Integralrechnung würde ich die Längen der Winkelhalbierenden als Radius von Kreissektoren annehmen. Dies ist aber nur eine Näherungslösung.
Bis demnächst
Matthias
Moin!
Meine mathematischen Fertigkeiten sind arg eingerostet, aber die Aufgabe hat mich gereizt. Nach diversen Sackgassen und Fehlern bin ich zu einer Lösung für die kleinsten Tortenstücke gekommen, für die größten würde ich bei ausreichend Elan sicher auch eine Lösung finden.
Ohne Integralrechnung, aber mit Berechnungen von Winkeln, Kreissektorflächen, Dreieckflächen etc. komme ich für die kleinsten Stücke auf 5,43%
Die Formel kann natürlich geliefert werden (auch mit nicht durch 0,2 ersetztem d), ist aber (auch ohne Herleitung) recht umfangreich und hier sicher nicht leicht darzustellen.
Viele Grüße, Norbert
Hallo Norbert K.,
der Wert 5,43% für die kleinsten Stücke ist korrekt.
Ich kenne deinen Weg dahin natürlich nicht, vermute aber, dass du für die größten Stücke nur geringfügige Änderungen vornehmen musst.
Viele Grüße ottogal
Hallo ottogal,
der Wert 5,43% für die kleinsten Stücke ist korrekt.
den kann ich bestätigen.
Ich kenne deinen Weg dahin natürlich nicht, vermute aber, dass du für die größten Stücke nur geringfügige Änderungen vornehmen musst.
11,79%
Bis demnächst
Matthias
11,79%
Bis demnächst
Matthias
Yep.
Hier mal noch ein paar Ergebnisse für andere Werte von d.
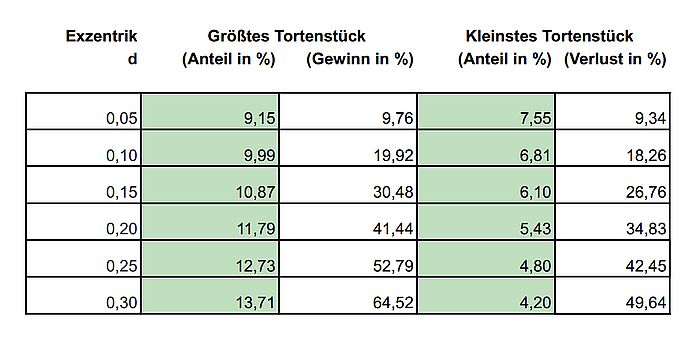
(Mit Gewinn bzw Verlust ist gemeint, um wieviel Prozent eines regulären Zwölftel-Tortenstücks man sich bei Wahl eines größten bzw. kleinsten verbessert bzw. verschlechtert.)
Jetzt also noch her mit den Formeln und ihrer Begründung...
Hallo ottogal,
Ich habe den Tortenteiler im Koordinatenursprung gelassen und die Torte nach unten (kleinstes Tortenstück) bzw. nach oben (größtes Tortenstück) verschoben. Zwei Schnitte des Tortenteilers liegen auf den Achsen. Der Tortenteiler ist auch groß genug, stets die ganze Torte zu teilen. Da Es 12 Stücke werden, beträgt der Winkel zwischen y-Achse und erstem Tortenstück 30°, mithin hat die entsprechende lineare Funktion den Anstiegswinkel von 60° und damit die Gleichung
$$ h(x) = \sqrt{3} \cdot x $$
Der obere „Halbkreis“ der Torte hat die Gleichung
$$ g(x) = \sqrt{ r^2 \pm x^2 } + d \cdot r $$
r - Radius,
d - Verschiebung
Bis demnächst
Matthias
Hallo Matthias,
kleine Typos:
Der obere „Halbkreis“ der Torte hat die Gleichung
$$ g(x) = \sqrt{ r^2 \pm x^2 } + d \cdot r $$
$$ g(x) = \sqrt{ r^2 - x^2 } + d \cdot r $$
- Fläche ist $$ \int_0^{x_s} (g(x)-h(x)),\mathrm dy $$
$$ \int_0^{x_s} (g(x)-h(x)),\mathrm dx $$
Der rechte Schnittpunkt hat die x-Koordinate
$$x_s = {{}\sqrt{3} d + \sqrt{4 - d^2} \over 4} * r$$
Man kann sich die mühsame Integration sparen, wenn man das (größtmögliche) Tortenstück als Summe einer Sektorfläche und einer Dreiecksfläche ermittelt:
Der zu dem Sektor gehörende Zentrumswinkel ist $$\alpha = \arcsin{x_s \over r}$$. Nimmt man ihn im Bogenmaß, so gilt das Verhältnis
$$Sektorfläche : Kreisfläche = \alpha : 2\pi$$
Mit der $$Kreisfläche = \pi r^2$$ hat der Sektor daher den Flächenwert
$$Sektor$$ = $${ 1\over 2}{\alpha} *r^2$$ = $${ 1\over 2} * {\arcsin{x_s \over r}}*r^2 = { 1\over 2} * {\arcsin{{}\sqrt{3} d + \sqrt{4 - d^2} \over 4}}*r^2$$.
Der Flächenwert des schmalen Dreiecks mit der Grundseite $$d*r$$ und der Höhe $$x_s$$ ist
$$Dreieck = {1 \over 2}drx_s = {1 \over 2}d*{{}\sqrt{3} d + \sqrt{4 - d^2} \over 4}*r^2$$.
Somit hat das größtmögliche Tortenstück den Flächenwert
$$T_1 = {1 \over 2}(\arcsin{{\sqrt{3}d + \sqrt{4 - d^2}} \over 4} + d{{\sqrt{3}d + \sqrt{4 - d^2}} \over 4})*r^2$$.
Division durch die Kreisfläche $$\pi r^2$$ ergibt dafür den Anteil
$${1 \over 2\pi}(\arcsin{{\sqrt{3}d + \sqrt{4 - d^2}} \over 4} + d{{\sqrt{3}d + \sqrt{4 - d^2}} \over 4})$$.
Analog geht die Rechnung für das kleinste Tortenstück (wobei man aber von einem Sektor ein Dreieck abzuziehen hat).
Hallo ottogal,
kleine Typos:
Der obere „Halbkreis“ der Torte hat die Gleichung
$$ g(x) = \sqrt{ r^2 \pm x^2 } + d \cdot r $$
$$ g(x) = \sqrt{ r^2 - x^2 } + d \cdot r $$
Minus für das kleinste Tortenstück, Plus für das größte.
$$ \int_0^{x_s} (g(x)-h(x)),\mathrm dx $$
Stimmt.
Man kann sich die mühsame Integration sparen, wenn man das (größtmögliche) Tortenstück als Summe einer Sektorfläche und einer Dreiecksfläche ermittelt:
Mit Technik ist da nichts mehr mühsam.
kleine Typos: ;-)
$$Sektor$$ = $${ 1\over 2}{\alpha} *r^2$$ = $${ 1\over 2} * {\arcsin{x_s \over r}}*r^2 = { 1\over 2} * {\arcsin{{}\sqrt{3} d + \sqrt{4 - d^2} \over 4}}*r^2$$
$$Sektor = { 1\over 2}{\alpha} \cdot r^2$$ = $${ 1\over 2} \cdot {\arcsin{x_s \over r}} \cdot r^2 = { 1\over 2} \cdot {\arcsin{{}\sqrt{3} d + \sqrt{4 - d^2} \over 4}} \cdot r^2$$.
$$Dreieck = {1 \over 2}drx_s = {1 \over 2}d*{{}\sqrt{3} d + \sqrt{4 - d^2} \over 4}*r^2$$.
$$Dreieck = {1 \over 2}d \cdot r \cdot x_s = {1 \over 2}d \cdot {{}\sqrt{3} d + \sqrt{4 - d^2} \over 4} \cdot r^2$$
usw.
Bis demnächst
Matthias
Minus für das kleinste Tortenstück, Plus für das größte.
Für das größte: $$g(x) = \sqrt{r^2 - x^2} + d \cdot r$$
Für das kleinste: $$g(x) = \sqrt{r^2 - x^2} - d \cdot r$$ oder $$g(x) = - \sqrt{r^2 - x^2} + d \cdot r$$ (je nachdem).
Unter der Wurzel steht in jedem Fall $$r^2 - x^2$$.
kleine Typos: ;-)
;-)) Das \cdot hatte ich übersehen.
Hallo ottogal,
Für das größte: $$g(x) = \sqrt{r^2 - x^2} + d \cdot r$$
Für das kleinste: $$g(x) = \sqrt{r^2 - x^2} - d \cdot r$$ oder $$g(x) = - \sqrt{r^2 - x^2} + d \cdot r$$ (je nachdem).
Das verschiebt den Tortenschneider.
Ich habe die Torte verschoben.
Bis demnächst
Matthias
Hallo Matthias,
Das verschiebt den Tortenschneider.
Nö.
Ich habe die Torte verschoben.
Ich auch.
Viele Grüße
ottogal
P.S. Es geht mir nicht um Rechthaberei - ich glaube schlicht, dass du dich irrst. Aber ich beende die Diskussion jetzt.
P.P.S. Schön, dass du die Lösung gefunden hast.
Hallo Norbert K.,
Die Formel kann natürlich geliefert werden (auch mit nicht durch 0,2 ersetztem d), ist aber (auch ohne Herleitung) recht umfangreich und hier sicher nicht leicht darzustellen.
Hier im Forum kannst du $$\LaTeX$$ zur Formeldarstellung benutzen.
Gruß
Julius