Mathematik zum Wochenende
- mathematik
Hallo alle,
einem Quadrat wird ein Viertelkreis einbeschrieben. Die Tangente in einem Punkt des Viertelkreises schneidet vom Quadrat ein Dreieck ab.
Berechne den Umfang dieses Dreiecks.
Bis demnächst
Matthias
Hallo Matthias,
die Vokabel „einbeschrieben“ hört man in der Mathematik oft, aber eine Definition dieser Vokabel macht sich rar.
In der Wikipedia habe ich bei Polygonzügen sinngemäß dies gefunden: Ein Polygonzug P (Quadrat) ist einer Kurve (Kreis) K einbeschrieben, wenn alle Stützpunkte von P auf K liegen.
Man findet auch Aufgaben über Quadrate oder Rechtecke, die einem Viertelkreis einbeschrieben sind, wobei eine Ecke des Rechtecks mit dem Mittelpunkt des Kreises zusammenfällt und die diagonal gegenüberliegende Ecke auf der Kreislinie liegt. Da wird aber vorausgesetzt, dass „einbeschrieben“ wohldefiniert ist.
Wäre dieser Viertelkreis hier nach deiner Vorstellung dem Quadrat einbeschrieben?
Wenn nicht - wie genau lautet die Definition von „einbeschrieben“?
Rolf
Hallo Rolf B,
die Vokabel „einbeschrieben“ hört man in der Mathematik oft, aber eine Definition dieser Vokabel macht sich rar.
Hm.
Wäre dieser Viertelkreis hier nach deiner Vorstellung dem Quadrat einbeschrieben?
Ja, aber für diese Aufgabe nicht. Ich hab also nicht genau genug formuliert. So ist das, wenn man nicht zu viel verraten möchte.
Bis demnächst
Matthias
@@Rolf B
Wäre dieser Viertelkreis hier nach deiner Vorstellung dem Quadrat einbeschrieben?
Ich denke, so ist’s gemeint:
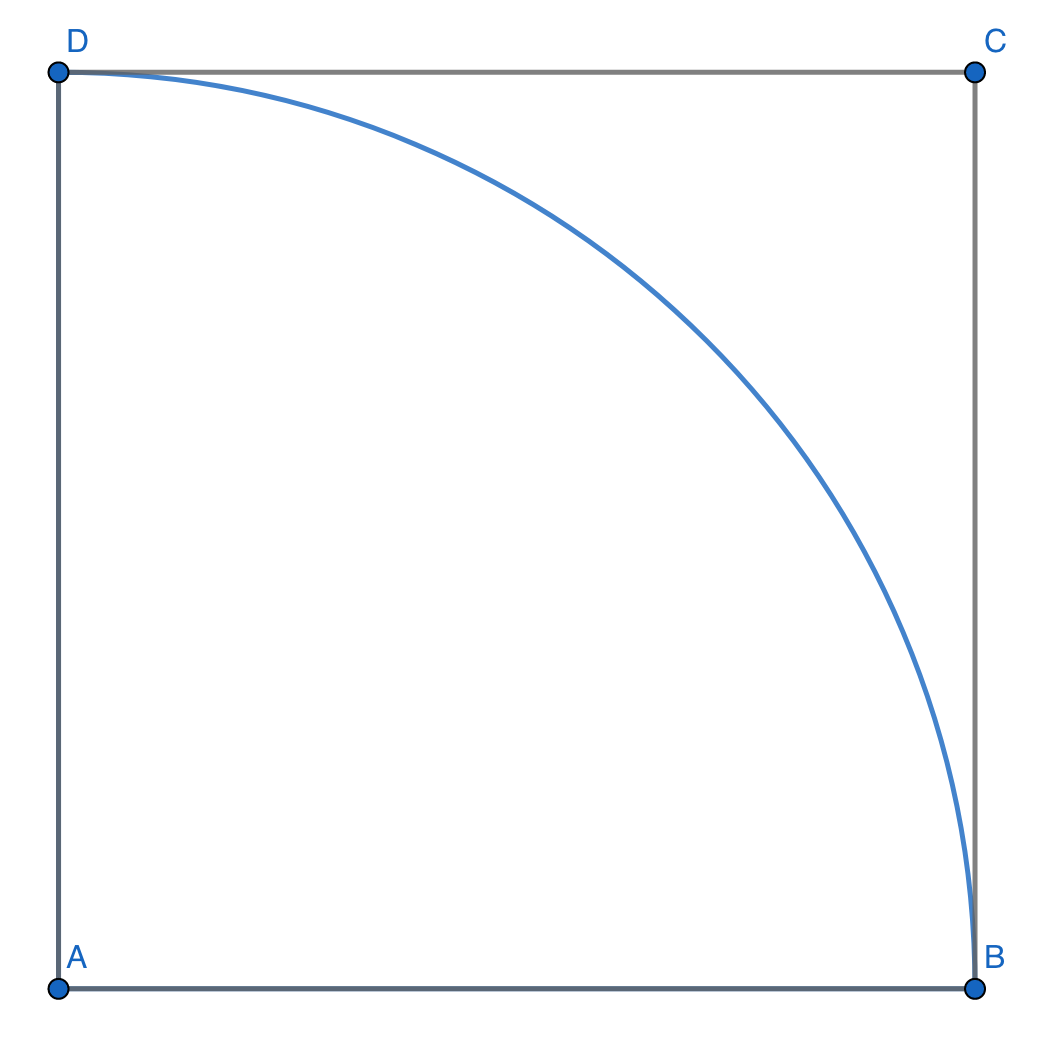
LLAP 🖖
Hallo Gunnar,
das habe ich mir für meine gleich danach eingereichte Lösung auch gedacht, aber die Korinthe hat gejuckt und wollte gekackt werden 💩…
(by the way, @Christian Kruse, gibt's eine Liste der Doppelpunkt−Codes für Emojis?)
Rolf
Hallo Rolf B,
das habe ich mir für meine gleich danach eingereichte Lösung auch gedacht, aber die Korinthe hat gejuckt und wollte gekackt werden 💩…
Und nicht unberechtigt.
Bis demnächst
Matthias
Hallo Matthias Apsel,
Und nicht unberechtigt.
Man könnte auch sagen: „In der Mathematik gibt es keine Korinthen.“
Bis demnächst
Matthias
Hallo Matthias Apsel,
einem Quadrat wird ein Viertelkreis einbeschrieben. Die Tangente in einem Punkt des Viertelkreises schneidet vom Quadrat ein Dreieck ab.
Berechne den Umfang dieses Dreiecks.
Die Aufgabenstellung ist nicht genau genug formuliert, wie @Rolf B korrekterweise anmerkt.
einem Quadrat mit der Seitenlänge a wird ein Viertelkreis mit dem Radius a einbeschrieben. Die Tangente in einem Punkt des Viertelkreises schneidet vom Quadrat ein Dreieck ab.
Berechne den Umfang dieses Dreiecks.
Bis demnächst
Matthias
@@Matthias Apsel
Wo wir gerade bei Quadraten und Kreisen und Tangenten sind, ein kleine Zusatzaufgabe:
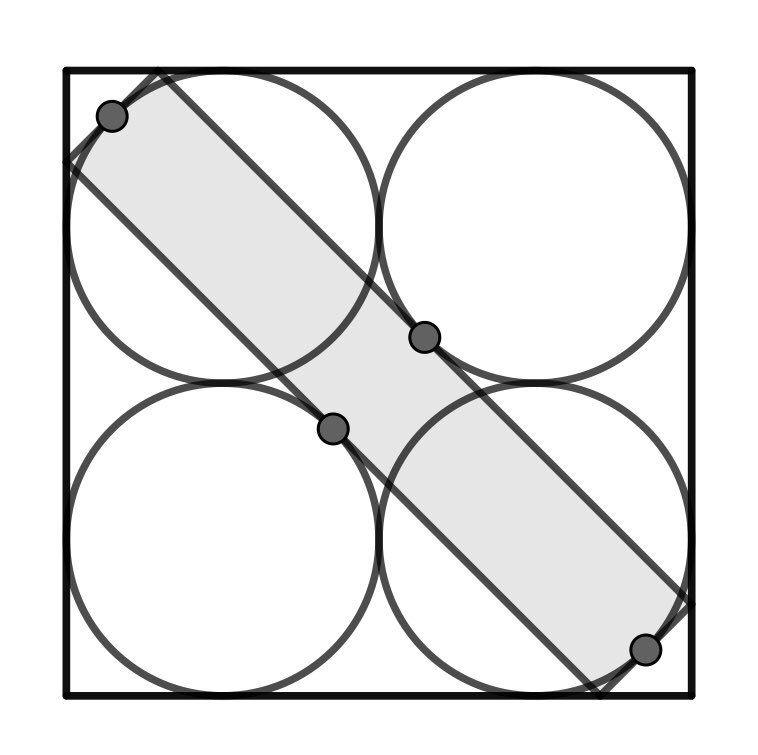
Wenn der Flächeninhalt des Quadrats 4 ist, wie groß ist der des grauen Rechtecks?
LLAP 🖖
@@Gunnar Bittersmann
Mich erreichten einige Lösungen, die am Ende die sog. „dritte binomische Formel“ verwendeten – ja, genau die, die keine binomische Formal ist. So hab ich’s auch gemacht. Aber:
Geht’s auch ohne zu rechnen zur Lösung?
LLAP 🖖
Hallo Gunnar,
definiere „ohne Rechnen“. Wenn ich sage, wegen XYZ ist dieses doppelt so groß wie jenes, dann rechne ich schon. Und ganz ohne Größenvergleiche oder Addition/Subtraktion von Teilflächen wird man kaum auskommen (ich bin bisher frei von Ahnung wie man ohne Binom3 weiter kommen sollte).
Hat du einen Ansatz? Oder ist das eine Frage auf die du selbst die Antwort suchst?
Rolf
@@Rolf B
Wenn ich sage, wegen XYZ ist dieses doppelt so groß wie jenes, dann rechne ich schon.
Wenn du das größere Stück in zwei Teile zerlegst und sagst, dass beide so groß sind wie jenes andere, dann rechnest du nicht.
LLAP 🖖
Mich erreichten einige Lösungen, die am Ende die sog. „dritte binomische Formel“ verwendeten – ja, genau die, die keine binomische Formal ist.
Seit wann das denn? $$a+b$$ ist ein Binom ebenso wie $$a-b$$, also ist es eine Formel über Binome...
@@ottogal
Mich erreichten einige Lösungen, die am Ende die sog. „dritte binomische Formel“ verwendeten – ja, genau die, die keine binomische Formal ist.
Seit wann das denn?
Schon immer, IMHO.
LLAP 🖖
Schon immer, IMHO.
LLAP 🖖
Selten eine so nutzlose Diskussion gesehen...
Hallo,
Selten eine so nutzlose Diskussion gesehen...
Du musst dringend häufiger hier im Forum lesen…
Scnr
Gruß
Kalk
Hallo Gunnar Bittersmann,
Wenn der Flächeninhalt des Quadrats 4 ist, wie groß ist der des grauen Rechtecks?
Wir zeichnen ein Paar Hilfslinien
und bezeichnen die Länge der roten Strecke mit x. Das Rechteck hat mithin die Breite 2_x_ und die Länge 2√2 - 2_x_. 2_x_ ergibt sich zu √2 - 1.
A = (2√2 - (√2 - 1)) ⋅ (√2 - 1)
A = (√2 + 1) ⋅ (√2 - 1)
A = 1.
Variante 2
Wenn man das alles schön auseinander schneiden würde, könnte man das Ausgangsquadrat zerlegen in 2 kleinere Quadrate und das Rechteck.
Das kleinere der beiden Quadrate hat eine Diagonalenlänge von √2 - 1, das größere der beiden eine Diagonalenlänge von √2 + 1. Dividiert man die Diagonalenlängen durch √2, erhält man die Seitenlängen, die Summe der Flächeninhalte ist 3.
Jetzt du. Ohne Rechnung.
Bis demnächst
Matthias
@@Matthias Apsel
A = (√2 + 1) ⋅ (√2 - 1)
Da isse, die dritte binomische Formel.
Jetzt du. Ohne Rechnung.
Nicht ich. @EratoSnail:
Man teilt das Rechteck EFGH in 3 Teile der Längen 1, b = EF und 1. Den ersten Teil lässt man, wo er ist; den letzten legt man rechtwinklig dazu in das Einheitsquadrat links oben. Den mittleren – ein Quadrat der Fläche b² – schneiden wir in vier Teile, welche genau in die Ecken passen (rot gekennzeichnet).
Die beiden rechteckigen Teile überdecken sich in einem Quadrat der Fläche b², was wir ausschneiden (grün gekennzeichnet) und ebenfalls in vier Teile schneiden, die – wie man leicht sieht 😉 – genau in die Zwischenräume passen. Damit hat EFGH denselben Flächeninhalt wie das Einheitsquadrat.
Jetzt wäre nur noch zu zeigen, dass das wirklich genau passt …
LLAP 🖖
PS: @ottogal hat noch eine andere Zerlegung gefunden; die Erklärung dazu enthält ebenfalls „was aber leicht zu sehen ist“. 😉
PS: @ottogal hat noch eine andere Zerlegung gefunden; die Erklärung dazu enthält ebenfalls „was aber leicht zu sehen ist“. 😉
Hier meine Zerlegungs-Lösung:
<zitat>
Ich zerlege ein Viertel des fraglichen Rechtecks in farbige Teilstücke:
und setze sie anderswo wieder zusammen:
Man erhält ein Quadrat mit Flächeninhalt 1/4, das große Rechteck hat daher den Flächeninhalt 1.
Für einen genauen Beweis muss man natürlich noch die Kongruenz gleichfarbiger Teilstücke nachweisen, was aber leicht zu sehen ist - das geht auch "ohne Rechnung" (sorry: „ohne Rechnung“)…
</zitat>
Ich trage noch nach, wie man die Kongruenz gleichfarbiger Teilstücke „leicht sieht“:
Grün:
Das grüne Stück bleibt an Ort und Stelle.
Gelb:
Without words
Rot:
Das cyan-farbene Dreieck ist kongruent zu dem danebenliegenden roten weil ihre Katheten gleichlange Tangenten-Abschnitte sind (rot markiert). Ansonsten: Without words.
Blau:
Die blauen Stücke werden jeweils durch eins der roten Dreiecke zu kongruenten Rechtecken ergänzt (deren Länge der Kreisradius ist).
Hallo Gunnar,
Jetzt wäre nur noch zu zeigen, dass das wirklich genau passt …
Da das Überlappungsquadrat und das Mittelpunktquadrat gleich groß sein müssen (es ist ja eine Kante gleich lang), ist eine Verteilung des Überlappungsquadrats auf die grünlichen Dreicke möglich, wenn die grünlichenen Dreiecke und die rötlichen Dreiecke (von denen eins nicht rötlich ist sondern irgend ein Pastellschmier) gleich groß sind.
Zu zeigen wäre, dass die Strecke GH und die Achteckseite unterhalb von H gleich lang sind. Ist das gegeben, ist das Dreieck HGD kongruent zu dem grünen Dreieck mit der oberen Ecke H. Denn dann sind alle Winkel gleich (wg. rechtwinklig und gleichschenklig) und eine Seite gleich lang.
Dass sie gleich sind, ergibt sich sofort aus der Here Be Dragons Diskussion in diesem Thread. Beide Teilstrecken liegen auf Tangenten, der Abstand ihrer Berührpunkte zu H muss also gleich sein, damit die Teilstrecken gleich lang.
Coole Lösung :)
Rolf
@@Rolf B
Zu zeigen wäre, dass die Strecke GH und die Achteckseite unterhalb von H gleich lang sind.
Moment, sollte nicht erst mal gezeigt werden, dass die Punkte E, F, G, H (die Schnittpunkte der Tangenten) auf den Seiten des großen Quadrats liegen?
Die Lösung mit der Berechnung von Länge und Breite des Rechtecks ist davon nicht ausgegangen; die Lösungswege mit Zerteilen und Zusammenfügen aber. Also müsste das erstmal gezeigt werden.
LLAP 🖖
Moment, sollte nicht erst mal gezeigt werden, dass die Punkte E, F, G, H (die Schnittpunkte der Tangenten) auf den Seiten des großen Quadrats liegen?
Das folgt unmittelbar aus den Symmetrien:
Die roten Tangenten in R bzw S liegen symmetrisch zur vertikalen Mittelachse a (da dies die Kreise und die Punkte R und S tun) und schneiden sich daher auf dieser.
b sei die Diagonale des gefärbten Teilquadrats. Die grüne Tangente in Q und die rote in R liegen spiegelbildlich zu b. Die Tangente in S ist ihr eigenes Spiegelbild bezüglich b und schneidet daher die grüne Tangente ebenfalls auf der Seite des gefärbten und damit auf der des großen Quadrats.
Hallo Gunnar,
Moment, sollte nicht erst mal gezeigt werden, dass die Punkte E, F, G, H (die Schnittpunkte der Tangenten) auf den Seiten des großen Quadrats liegen?
Da jeweils eine der beteiligten Tangenten mit einer Quadratseite zusammenfällt, bleibt dem Schnittpunkt wohl nicht viel anderes übrig als auf der Quadratseite zu liegen. Es sei denn, er läge zwar auf der Tangente, aber außerhalb des Quadrats - das ist auf Grund der Lage der diagonalen Tangente aber nicht möglich
Rolf
Hallo Matthias Apsel,
einem Quadrat wird ein Viertelkreis einbeschrieben. Die Tangente in einem Punkt des Viertelkreises schneidet vom Quadrat ein Dreieck ab.
Berechne den Umfang dieses Dreiecks.
Weil die Tangente senkrecht auf ihrem Berührungsradius steht, sind die Vierecke ABQP und APRD symmetrische Drachenvierecke. Mit den gewählten Bezeichnungen a für die Seitenlänge des Quadrates und x bzw. y ergibt sich für den Umfang u = a-x + a-y + x + y = 2_a_.
Richtige Lösungen gab es von @Gunnar Bittersmann, @Rolf B, @encoder, @Tabellenkalk und @ottogal.
Bis demnächst
Matthias
Bevor ich auch auf die eigentlich ins Auge springende Lösung von Matthias gekommen bin, hatte ich umständlich mit Trigonometrie herumgerechnet. Freilich ergab das keine wettbewerbsfähige Lösung - vielleicht interessiert sie trotzdem den einen oder andern.
(Beim Ausformulieren merkt man schnell, dass man unbedingt abkürzende Variablen verwenden sollte; aber das ist eigentlich ein Haupttrick in der Mathematik.)
Also los:
Das Quadrat habe die Seitenlänge 1.
Sei $$\alpha = \angle EAP$$.
Da die Tangente in P auf $$AP$$ senkrecht steht, ist auch $$\angle CST = \alpha$$ (Winkel mit paarweise orthogonalen Schenkeln sind gleich),
und als Stufenwinkel an Parallelen ist auch $$\angle FPT = \alpha$$.
Wir definieren zwecks Abkürzung:
$$s = \sin(\alpha)$$
$$c = \cos(\alpha)$$
$$t = \tan(\alpha)$$
Bekanntlich gelten dann die Beziehungen
(1) $$t=s/c$$ und
(2) $$s²+c²=1$$.
Mit den gemäß der Zeichnung benannten Punkten setzen wir
$$x = TC$$, $$y= CS$$ und $$z = TS$$.
Dann gilt:
$$AE=c$$ und daher $$FC=EB=1-c$$
$$PE=s$$ und daher $$PF=1-s$$
Nun ist $$\frac{TF}{PF}=t$$, somit $$TF=t \cdot PF = t(1-s)=\frac{s-s²}{c}$$ (wegen (1)) und
$$x=TC=TF+FC=\frac{s-s²}{c}+(1-c)=\frac{s-s²+c-c²}{c}$$, also wegen (2)
$$x=\frac{s+c-1}{c}$$.
Mit der Abkürzung $$d=s+c-1$$ vereinfachen wir das Folgende.
Wir erhalten $$x=\frac{d}{c}$$, und wegen $$\frac{x}{y}=t$$ daraus (mit (1))
$$y=\frac{x}{t}=\frac{xc}{s}$$, also $$y=\frac{d}{s}$$.
Pythagoras im Dreieck $$TSC$$ ergibt nun
$$z²=x²+y²=d² \cdot \left( \frac{1}{c²}+\frac{1}{s²} \right)=d² \cdot \frac{s²+c²}{c²s²}$$, also wegen (2)
$$z²=\left( \frac{d}{cs} \right)²$$ und damit $$z=\frac{d}{cs}$$.
Der Umfang des Dreiecks $$TSC$$ ist daher
$$u=x+y+z=\frac{d}{c}+\frac{d}{s}+\frac{d}{cs}=d \cdot \frac{s+c+1}{sc}=\frac{(s+c-1)(s+c+1)}{sc}=\frac{(s+c)²-1²}{sc}=\frac{s²+2sc+c²-1}{sc}$$, also mit (2)
$$u=\frac{2sc}{sc}=2$$.
Also ist unabhängig vom Winkel $$\alpha$$ der Umfang des Dreiecks stets $$u=2$$, also das Doppelte der Quadratseite.
@@ottogal
Bevor ich auch auf die eigentlich ins Auge springende Lösung von Matthias gekommen bin
Ich hab meine Augen erfolgreich davor geschützt, dass mir da was reinspringt. 😎
hatte ich umständlich mit Trigonometrie herumgerechnet.
Ich bin jetzt nicht jeden einzelnen Schritt durchgegangen, hab aber einiges wiedererkannt. Ich glaube, ich hab’s so ähnlich, wenn nicht gar genauso gemacht:
O.B.d.A.: Seitenlänge des Quadrats ABCD 1, Viertelkreis um A, darauf Punkt P.
Tangente in P schneidet BC in Q und CD in R.
S und T Fußpunkte der Lote von P auf BC bzw. CD.
∠BAP = φ, ebenso groß sind ∠CQR und ∠TPR.
Es ist DT = cos φ = c und BS = sin φ = s. Folglich TC = 1 − c und PT = SC = 1 − s.
tan φ = RT/PT, also RT = s/c (1 − s).
RC = s/c (1 − s) + 1 − c = 1/c (s − s² + c − c²) = 1/c (s + c − 1).
tan φ = RC/QC, folglich QC = c/s RC = 1/s (s + c − 1).
sin φ = RC/RQ, folglich RQ = 1/s RC = 1/sc (s + c − 1).
Umfang: (1/c + 1/s + 1/sc) (s + c − 1) = 1/sc (s + c + 1) (s + c − 1) = 1/sc ((s + c)² − 1) = 1/sc (s² + 2sc + c² − 1) = 1/sc (1 + 2sc − 1) = 2.
Oder geht’s mal wieder noch viel einfacher?
Ja, geht.
LLAP 🖖
Ja, geht.
Ei wie denn?
@@ottogal
Ja, geht.
Ei wie denn?
Matthias hat einen Drachen für uns gebaut.
LLAP 🖖
Ach so meintest du das. Ich dachte, du hast noch eine einfachere trigonometrische Lösung gefunden.
Hallo ottogal,
ich bin beeindruckt, dass Du das durchgezogen hast! Ich war schon halbwegs gestartet, ähnliches zu tun, und dann hat mich der Ansatz dermaßen gegruselt, dass ich lieber nach einem Achtklässlerkompatiblen Weg gesucht und Matthias' Lösung gefunden habe :)
Rolf
Pythagoras im Dreieck $$TSC$$ ergibt nun
$$z²=x²+y²=d² \cdot \left( \frac{1}{c²}+\frac{1}{s²} \right)=d² \cdot \frac{s²+c²}{c²s²}$$, also wegen (2)
$$z²=\left( \frac{d}{cs} \right)²$$ und damit $$z=\frac{d}{cs}$$.
Statt über den Pythagoras bekommt man $$z$$ direkt über $$\frac{x}{z}=s$$ zu
$$z=\frac{x}{s}=\frac{d}{cs}$$.
Hallo,
Weil die Tangente senkrecht auf ihrem Berührungsradius steht, sind die Vierecke ABQP und APRD symmetrische Drachenvierecke.
Von den Drachen habe ich nur die gleichschenkligen „Dreiecke“ mit den gebogenen Grundflächen benötigt. Wenn man sich vorher noch die entarteten Dreiecke in den Extremen anschaut, kommt man ohne Rechnung aus…
Gruß
Kalk
Hallo Tabellenkalk,
dann führe bitte mal einen Beweis, dass sie gleichschenklig sind, ohne auf den Rest der Drachen zurückzugreifen.
Rolf
Hallo,
Hallo Tabellenkalk,
dann führe bitte mal einen Beweis, dass sie gleichschenklig sind, ohne auf den Rest der Drachen zurückzugreifen.
Rolf
Äh, kA ob und wie ich das beweisen muss für diese Aufgabe. Aber der Schnittpunkt zweier Tangenten desselben Kreises muss von beiden Berührpunkten gleich weit entfernt sein.
Gruß
Kalk
Hallo Tabellenkalk,
Aber der Schnittpunkt zweier Tangenten desselben Kreises muss von beiden Berührpunkten gleich weit entfernt sein.
Ich beweise das mal für Dich. Das ist so ein typischer Banalbeweis, wo die Schwierigkeit in der Frage liegt, was man da eigentlich beweisen muss :)
Seien B₁ und B₂ Punkte auf dem Umfang des Kreises um M. Bei B₁ und B₂ seine Tangenten an den Kreis angetragen. T sei der Schnittpunkt dieser Tangenten. Der Fall, dass M, B₁ und B₂ auf einer Geraden liegen, wird nicht betrachtet, da die Tangenten dann parallel sind und kein Schnittpunkt T existiert. Die oben stehende Skizze zeigt den Fall, dass der Winkel B₂MB₁ kleiner als 180° ist. Ist er größer, stelle man sich das Bild gespiegelt vor. Für den Beweis ist das unerheblich.
Die Winkel MB₁T und MB₂T sind rechte, weil sie von einem Radius und einer Tangente gebildet werden. B₁ und B₂ liegen auf dem Kreisumfang, daher entspricht die Länge der Strecken MB₁ und MB₂ dem Kreisradius. Die Dreiecke MTB₁ und MTB₂, mit der gemeinsamen Seite MT, besitzen also zwei gleiche Seiten und einen - der längeren Seite gegenüberliegenden - gleichen Winkel und sind damit SSW-kongruent. Daraus folgt TB₁ = TB₂.
Ja, und da isser, der Drache.
Rolf
Hallo,
Ja, und da isser, der Drache.
Also Frage in die Runde: muss ich, um die Aufgabe zu lösen, den Drachen beweisen oder darf ich die Gleichschenkligheit als banal gegeben voraussetzen?
Gruß
Kalk
Hallo Tabellenkalk,
Also Frage in die Runde: muss ich, um die Aufgabe zu lösen, den Drachen beweisen oder darf ich die Gleichschenkligheit als banal gegeben voraussetzen?
Ich würde sagen, das muss man nicht beweisen.
Bis demnächst
Matthias
Hallo Rolf B,
Ja, und da isser, der Drache.
Der Drachen. Wenn man diese beiden Wörter deklinieren soll, muss man 14 Mal „Drachen“ schreiben.
Bis demnächst
Matthias
@@Matthias Apsel
Ja, und da isser, der Drache.
Der Drachen. Wenn man diese beiden Wörter deklinieren soll, muss man 14 Mal „Drachen“ schreiben.
Du hast einen Drachen für mich gebaut – eins meiner Lieblingslieder von Sebastian Krämer. Passt gut zur Jahreszeit. 😆 /cc @Christian Kruse
LLAP 🖖
Hallo Gunnar Bittersmann,
Du hast einen Drachen für mich gebaut – eins meiner Lieblingslieder von Sebastian Krämer. Passt gut zur Jahreszeit. 😆 /cc @Christian Kruse
Cool. Das kannte ich noch nicht.
Bis demnächst
Matthias
Hallo Rolf B,
dann führe bitte mal einen Beweis, dass sie gleichschenklig sind, ohne auf den Rest der Drachen zurückzugreifen.
Von einem Punkt P außerhalb eines Kreises k mit dem Mittelpunkt K sollen die Tangenten konstruiert werden.
Bis demnächst
Matthias