@@Gunnar Bittersmann
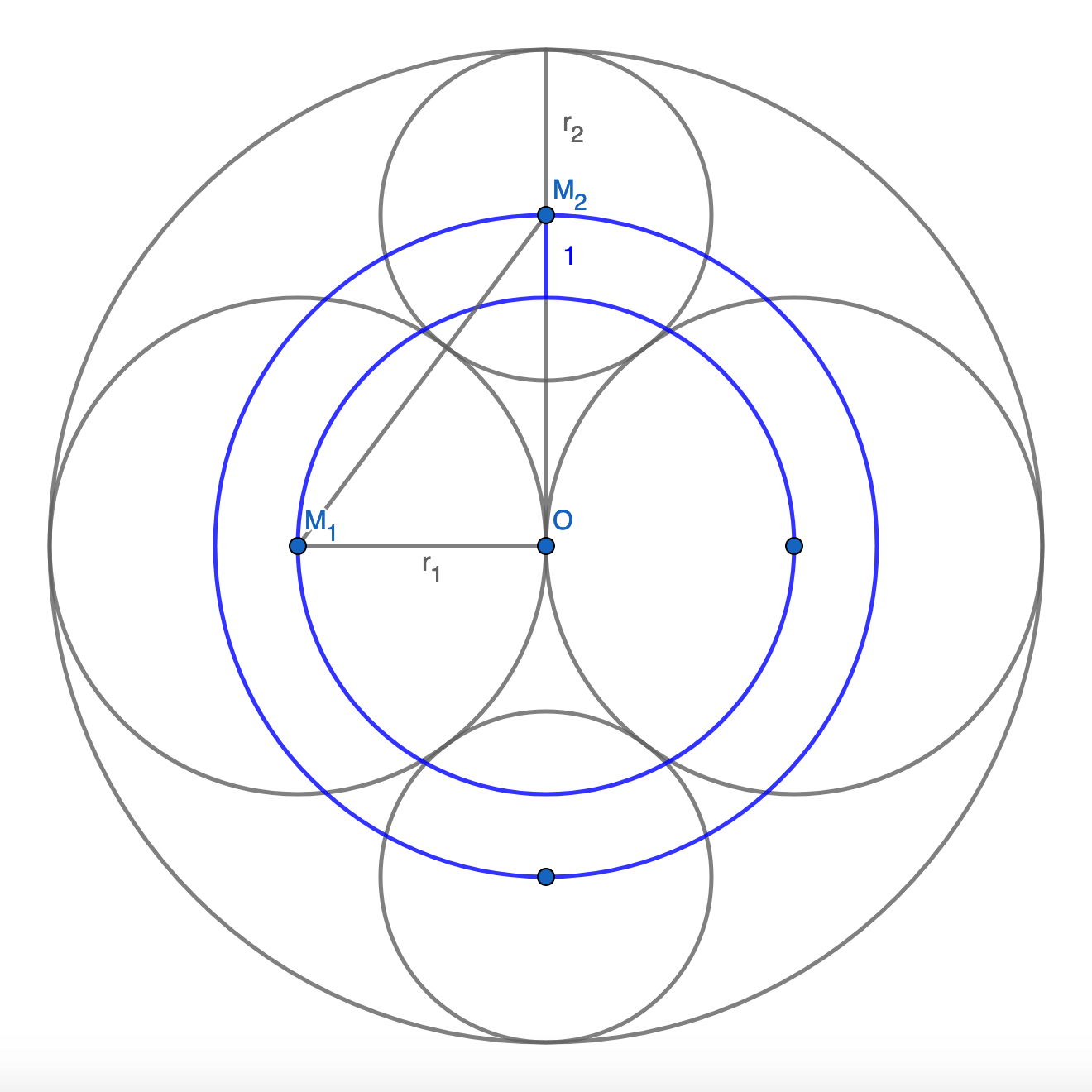
r₁ und r₂ Radien der großen bzw. kleinen einbeschriebenen Kreise.
Radius des Außenkreises: 2r₁ = r₁ + 1 + r₂, woraus r₂ = r₁ − 1 folgt.
△M₁OM₂ wegen Symmetrie rechtwinklig; Pythagoras: r₁² + (r₁ + 1)² = (r₁ + r₂)² = (2r₁ − 1)².
Auflösung der quadratischen Gleichung ergibt r₁ = 3.
Fläche des Kreisrings mit Innenradius r₁ = 3 und Außenradius r₁ + 1 = 4 ist (4² − 3²) × π = 7π.
LLAP 🖖
--
„Man kann sich halt nicht sicher sein“, sagt der Mann auf der Straße, „dass in einer Gruppe Flüchtlinge nicht auch Arschlöcher sind.“
„Stimmt wohl“, sagt das Känguru, „aber immerhin kann man sich sicher sein, dass in einer Gruppe Rassisten nur Arschlöcher sind.“
—Marc-Uwe Kling
„Man kann sich halt nicht sicher sein“, sagt der Mann auf der Straße, „dass in einer Gruppe Flüchtlinge nicht auch Arschlöcher sind.“
„Stimmt wohl“, sagt das Känguru, „aber immerhin kann man sich sicher sein, dass in einer Gruppe Rassisten nur Arschlöcher sind.“
—Marc-Uwe Kling


