Mathematik zur Wochenmitte
- mathematik
Nanu, ist der @Rolf B gar nicht im Urlaub? Oder ist Das Abhängen in diesem Forum für ihn Urlaub? 🤔
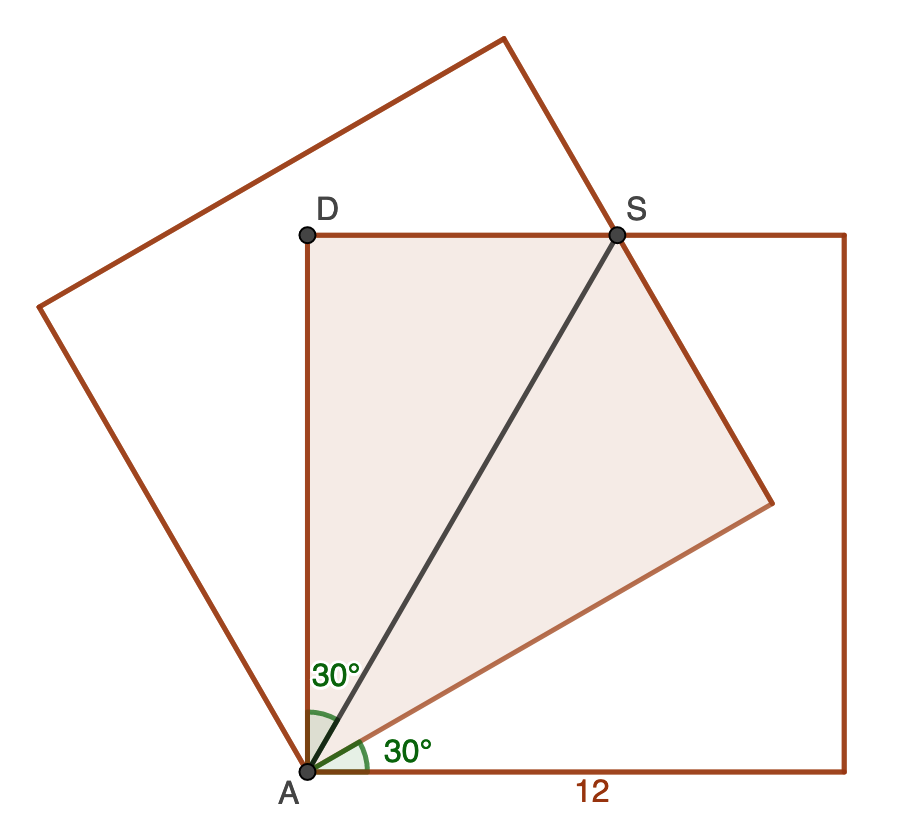
Na denn: zwei Quadrate mit Seitenlänge 12, eins um 30° gedreht. Wie groß ist die schraffierte Fläche?
😷 LLAP
Hallo Gunnar,
klar hab ich Urlaub, heute beste Grillsaison auf 3000m (viele knallrot gebrannte Skirutscher gesehen)
Ob ich aber Nerv habe, mir den Kopf zu zerbrechen?
Rolf
überschlagen ** quadrat(e)
Gruß, Alexander
@@Alexander Hein
überschlagen ** quadrat(e)
Als Überschlag in der richtigen Größenordnung; als Lösung zu weit vom richtigen Wert weg.
Lösungen bitte nicht hier posten, sondern per DM an mich. Ich löse dann in ein paar Tagen auf.
😷 LLAP
Hallo Gunnar,
zu weit vom richtigen Wert weg.
Wie?!?! Ich hab den gleichen Wert raus.
Bei näherer Betrachtung hab ich da aber wohl was verwechselt. Jetzt schickst Du mich als Reißbrett zurück, dabei hab ich doch URLAUB!
Rolf
Lieber Rolf,
Jetzt schickst Du mich als Reißbrett zurück,
wärst Du lieber ein Nudelholz?
Liebe Grüße
Felix Riesterer
Hi,
Jetzt schickst Du mich als Reißbrett zurück,
wärst Du lieber ein Nudelholz?
scheint so, als hätte außer uns kaum jemand den Tippfehler bemerkt. Laut openstreetmap.org gibt es übrigens etwa 2km von meinem Zuhause entfernt ein Reisbüro. Bei den Schwaben hätte ich eher ein Spätzlebüro erwartet. 😉
Immer eine Handbreit Wasser unterm Kiel
Martin
Hi,
Jetzt schickst Du mich als Reißbrett zurück,
wärst Du lieber ein Nudelholz?
scheint so, als hätte außer uns kaum jemand den Tippfehler bemerkt.
Du meinst das fehlende zweite l in Nudellholz? ;-)
Ich hab zuerst Reißbett gelesen (Jürgen Drews: ein Bett im Reisfeld ...)
Laut openstreetmap.org gibt es übrigens etwa 2km von meinem Zuhause entfernt ein Reisbüro.
hier in der Nähe gibt's eine ehemalige Reismühle
cu,
Andreas a/k/a MudGuard
Hallo,
Ich hab zuerst Reißbett gelesen
auch nicht schlecht. 😀
(Jürgen Drews: ein Bett im Reisfeld ...)
Ich kenn den Song eher als Ein Korn im Feldbett.
Laut openstreetmap.org gibt es übrigens etwa 2km von meinem Zuhause entfernt ein Reisbüro.
hier in der Nähe gibt's eine ehemalige Reismühle
Das scheint aber wirklich so gemeint zu sein - anders als beim hiesigen Reisebüro.
Immer eine Handbreit Wasser unterm Kiel
Martin
Hi,
Ich kenn den Song eher als Ein Korn im Feldbett.
Die Prinzessin auf dem Korn?
cu,
Andreas a/k/a MudGuard
Hi,
Ich hab zuerst Reißbett gelesen
früher auch Streckbank genannt …
cu,
Andreas a/k/a MudGuard
@@Rolf B
Jetzt schickst Du mich als Reißbrett zurück
Du kannst auch mit Stöckchen im Schnee malen …
😷 LLAP
Hi,
Lösungen bitte nicht hier posten, sondern per DM an mich. Ich löse dann in ein paar Tagen auf.
Das solltest Du halt ins Startposting eines Rätsel-Threads schreiben.
cu,
Andreas a/k/a MudGuard
@@MudGuard
Lösungen bitte nicht hier posten, sondern per DM an mich. Ich löse dann in ein paar Tagen auf.
Das solltest Du halt ins Startposting eines Rätsel-Threads schreiben.
Ja, da hast du natürlich recht.
Für gewöhnlich machen bei den Matherätseln immer dieselben paar Leute mit, die das wissen. Schön, wenn auch andere hinzukommen.
😷 LLAP
Hi,
Für gewöhnlich machen bei den Matherätseln immer dieselben paar Leute mit, die das wissen.
Die werden aber damit leben können, wenn der Hinweis dabeisteht.
Schön, wenn auch andere hinzukommen.
Da stimme ich Dir zu.
cu,
Andreas a/k/a MudGuard
Hallo Alexander,
ich habe deinen Lösungswert wegeditiert.
Lösungsversuche bitte als Nachricht an den Autor schicken.
Ein gültiger Lösungsversuch sollte eine mathematisch fundierte Herleitung oder Begründung enthalten und nicht eine Schätzung darstellen, oder durch Abzählen oder Abmessen von Pixeln entstehen.
Der Autor löst irgendwann auf und sagt, wer teilgenommen hat und ob die Lösung brauchbar war.
Rolf
@@Gunnar Bittersmann
Es geht aufs Wochenende zu. Vorher noch schnell die Lösung. 🤣
😷 LLAP
@@Tabellenkalk
die Lösung. 🤣
Kann man machen...
Nicht wahr? 🤣
Einfacher geht so: Die Figur ist symmetrisch zur Achse AS.[1] Daraus ergibt sich ∡DAS = 30°, DS/AD = tan 30° = ⅓√3. Mit AD = 12 ist DS = 4√3.
Die gesuchte Fläche ist das Doppelte von ▵ASD, also AD × DS = 48√3.
Oder auch ohne Winkelfunktion, wie du @Tabellenkalk es gemacht hast:
😷 LLAP
Nachtrag: Die beiden Dreiecke stimmen in einer Seite der Länge 12, der gemeinsamen Seite AS sowie dem rechten Winkel überein, sind also nach SSW kongruent. ↩︎
Das blaue Parallelogrammm lässt sich in 4 zueinander kongruente rechtwinklige Dreiecke zerlegen. Mit 2 davon lässt sich einerseits der gesuchte Drachen, andererseits ein gleichseitiges Dreieck zusammensetzen:
Für Grundseite a und Höhe h eines gleichseitigen Dreiecks gilt $$h = \frac{\sqrt{3}}{2} a$$ oder $$a = \frac{2 \sqrt{3}}{3} h$$,
sein Flächeninhalt ist daher $$\frac{1}{2} a h = \frac{\sqrt{3}}{3} h^2$$.
Für $$h = 12$$ erhält man also $$48 \sqrt{3}$$, auch für den Drachen.
Hallo ottogal,
Die Begründung, warum das Dreieck gleichseitig und nicht lediglich gleichschenklig ist, fehlt.
Oder andersrum: warum erzeugt das "Ausklappen" des Drachen ein Parallelogramm, genauer: eine Raute. Das passiert nicht bei jedem Drachen.
Das ist mit den 30° und einem Sinus schnell getan, aber tun muss man es, meine ich.
Rolf
@@Rolf B
Die Begründung, warum das Dreieck gleichseitig und nicht lediglich gleichschenklig ist, fehlt. […]
Das ist mit den 30° und einem Sinus schnell getan
Da brauchst du keine Winkelfunktion zu. Wie man leicht sieht, setzt sich das Ding aus zwei 30°-60°-90°-Dreiecken zusammen, hat also drei 60° große Innenwinkel.
😷 LLAP