Mathematik zum Wochenende
- mathematik
Bei @Five_Triangles eine Aufgabe von Catriona Shearer gefunden, die sich als Wochenendknobelei ganz nett macht:
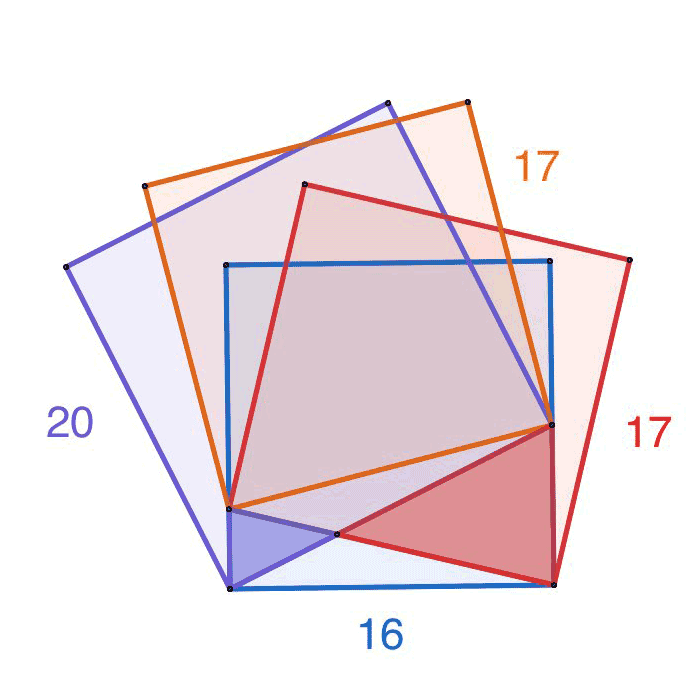
Die Zahlen geben die Flächeninhalte der jeweiligen Quadrate an. Wie groß ist die Differenz der Flächeninhalte der farblich markierten Dreiecke?
Erwähnte ich schon, dass man das ohne Pythagoras lösen sollte?
Und wie sie so schön schreiben, kann man die Zeichnung weiter ausmelken:
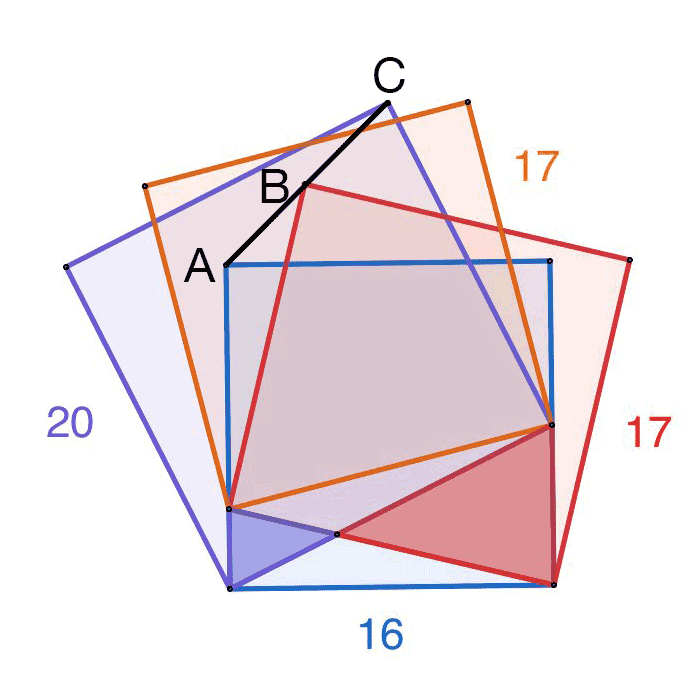
Zeige, dass A, B und C auf einer Linie liegen, und berechne das Verhältnis AB : BC.

Zeige, dass die markierte Quadratseite und die eingezeichnete Linie durch die zwei Eckpunkte parallel sind.
LLAP 🖖
Keine Lösung sondern eine Frage. Sehs leider erst heute.
Ich wollte mit dem Pythagoras nachsehen ob die Seitenlängen wirklich so schön gerade sein können und sich alles da berührt wo ich es herauslese.
Die senkrechte Seite des roten Dreiecks (rechts) berechnet sich mit den Seiten 16 und 20 zu genau 12.
Da das Dreieck nach rechts rüber zwei gleiche Seiten mit 17 hat, müsste deshalb die senkrechte Seite des blauen Dreiecks die Hälfte der roten, also 6 betragen.
Der Pythagoras mit den Seiten 16 und 17 ergibt für diese Seite aber Wurzel(33).
Wo liegt der Fehler?
Hallo encoder,
Wo liegt der Fehler?
Die Zahlen bezeichnen die Flächeninhalte.
Bis demnächst
Matthias
ach je... da sieht man mal wohin Urlaub die Gedanken führt!
@@encoder
… mit den Seiten 16 und 20 …
Wo liegt der Fehler?
Hier: „Die Zahlen geben die Flächeninhalte der jeweiligen Quadrate an.“
LLAP 🖖
@@encoder
Sehs leider erst heute.
Na dann warte ich noch ein wenig mit der Auflösung.
LLAP 🖖
@@Gunnar Bittersmann
Na dann warte ich noch ein wenig mit der Auflösung.
So, genug gewartet. @encoder sollte die Lösung inzwischen gefunden haben – sie geht genauso wie seine/ihre Lösung vom Februar:

Wir zerlegen das Quadrat EBFG mit Parallelen zu AB und AD in 4 Dreiecke und ein Quadrat.
Mit AB = 4 und AE = a ergibt sich für den Flächeninhalt von EBFG:
17 = 4 × ½ × 4a + (4 − a)² = 8a + 16 − 8a + a²
17 = 16 + a²
Das ist genau das, was einem mit Pythagoras auch ins Auge springt, nur eben ohne.
AE = a = 1.
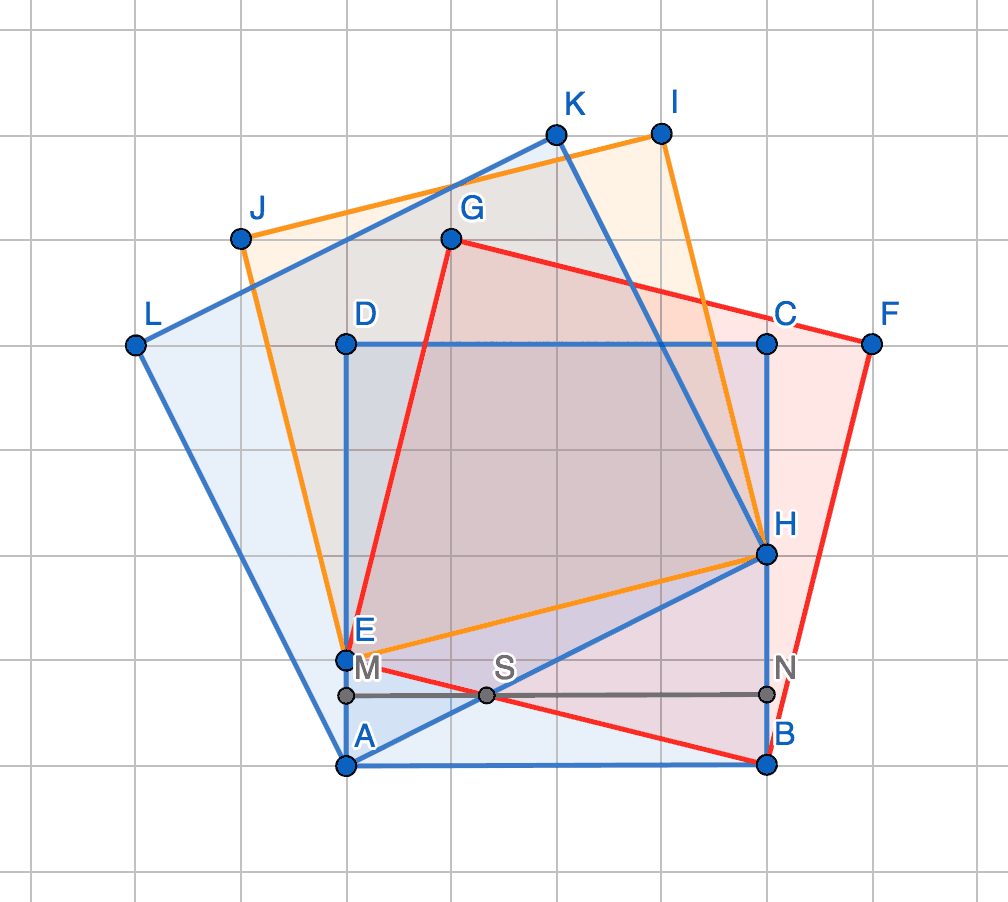
Analog lässt sich so über den Flächeninhalt von AHKL auch BH = b bestimmen:
20 = 4 × ½ × 4b + (4 − b)² = 8b + 16 − 8b + b² = 16 + b²
BH = b = 2
Darauf kommt man aber auch über EB = EH wegen der Flächengleichheit von EBFG und EHIJ.
S Schnittpunkt von AH und EB;
M, N Fußpunkte der Lote von S auf AE und BH
Die Dreiecke SEA und SBH sind änhlich. (Die Innenwinkel sind Scheitelwinkel bzw. Wechselwinkel an geschnittenen Parallelen.)
SM : SN = AE : BH = 1 : 2, wegen SM + SN = 4 ist SM = ⁴⁄₃
Flächeninhalt von SEA ist ½ × 1 × ⁴⁄₃ = ⅔, Flächeninhalt von SBH ist 4mal so groß.
Die gesuchte Differenz der Flächen ist demnach 3 × ⅔ = 2.

Zusatzaufgaben: Wir legen ein Koordinatensystem so, dass A im Ursprung liegt und D(0, 4) ist.
Dann ist E(0, 1) und G(1, 5) sowie H(4, 2) und I(3, 6), K(2, 6), L(−2, 4).
Man sieht, dass D, G und K auf einer Linie liegen und dass DG = GK ist.
Die Gerade GI hat den Anstieg ½, ebenso wie die Gerade LK, sie sind also parallel.
Hat jemand eine Lösung ohne Rechnen mit Koordinaten, sondern rein geometrisch?
LLAP 🖖
Hallo in die Runde!
Wir zerlegen das Quadrat EBFG mit Parallelen zu AB und AD in 4 Dreiecke und ein Quadrat.
Oder mit einer Zerlegung in ein Parallelogramm und zwei kongruente Dreiecke:
Sei PQ = d.
Mit AB = 4 und AE = a ergibt sich für das Parallelogramm der Flächeninhalt
(4 + d) × (4 − a) und für die beiden Dreiecke zusammen
(4 + d) × a, für die Gesamtfläche also (4 + d) × 4 = 16 + 4d.
Dies muss 17 sein, also ist 4d = 1.
Nach dem Höhensatz ist aber 4d = a², somit it a = 1.
Entsprechend zeigt man, dass BH = b = 2 ist:
Zusatzaufgaben:
Hat jemand eine Lösung ohne Rechnen mit Koordinaten, sondern rein geometrisch?
Ich benenne die Punkte (außer S) wie in deiner Lösung:
Sei S der Schnittpunkt von AD mit LK. Da die Winkel <LAS und <BAH gleich sind - sie ergänzen jeweils <HAS zu einem Rechten - sind die rechtwinkligen Dreiecke LAS und BAH ähnlich. DA HB = AB/2 ist, folgt SL = LA/2 = LK/2. S ist daher der Mittelpunkt von LK.
Wegen der Kongruenz der roten Dreiecke EAB, BQF, FRG und GTE ist BQ = EA = 1, also AQ = AT = 5 und daher T derselbe Punkt wie S.
Folglich sind SG und LD parallel, und nach dem Strahlensatz folgt
KD : KG = KL : KS = 2 : 1, also GD : KG = 1 : 1.
Die fünf farbigen rechtwinkligen Dreiecke sind kongruent (mit den Kathetenlängen 1 und 4). Daher sind die Strecken GP und IH gleich lang und parallel, d.h. PHIG ist ein Parallelogramm. Es folgt: GI ist parallel zu PH und daher auch zu LK.
Ganz zu Anfang vergessen: Sei PQ = d.
@@ottogal
Ganz zu Anfang vergessen: Sei PQ = d.
Ich setze es gleich mal rein.
LLAP 🖖