Mathematik zum Wochenende/Wochenanfang

[Gunnar Bittersmann]

Zwei Aufgaben; eine zum Wochenende, eine zum Wochenanfang; beide mit gleichseitigen Dreiecken und Kreisen und Verhältnissen von Flächen:

1. Ein gleichseitiges Dreieck kann man mit 1, 1 + 2, 1 + 2 + 3 usw., also 1 + 2 + 3 + … + n Kreisen derart füllen:

   

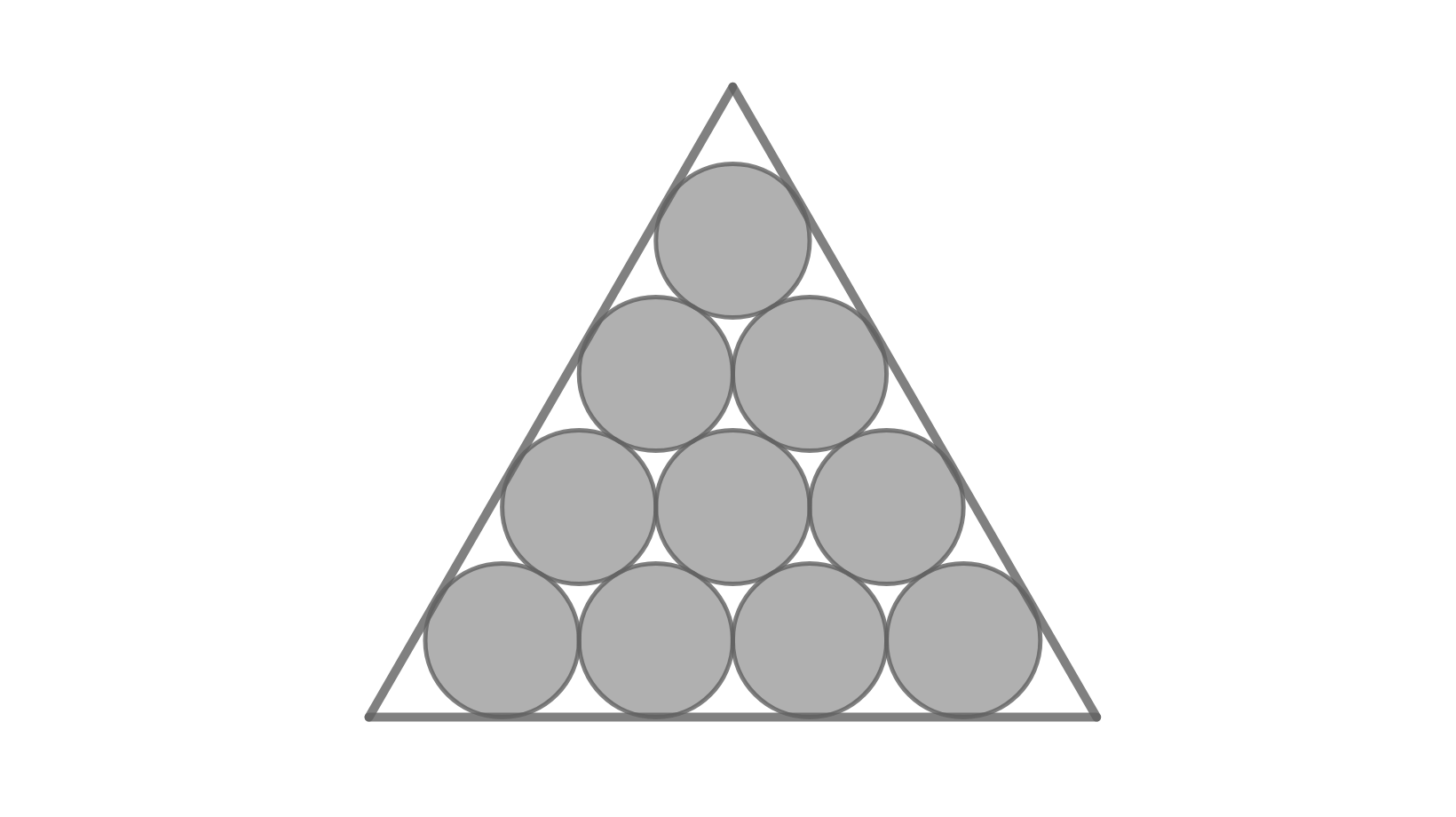
   Wie ist das Verhältnis der schraffierten Fläche der Kreise zur Fläche des Dreiecks für n → ∞?

   ---

2. Wie ist das Verhältnis der schraffierten Fläche der Dreiecke zur Fläche des großen Dreiecks?

   

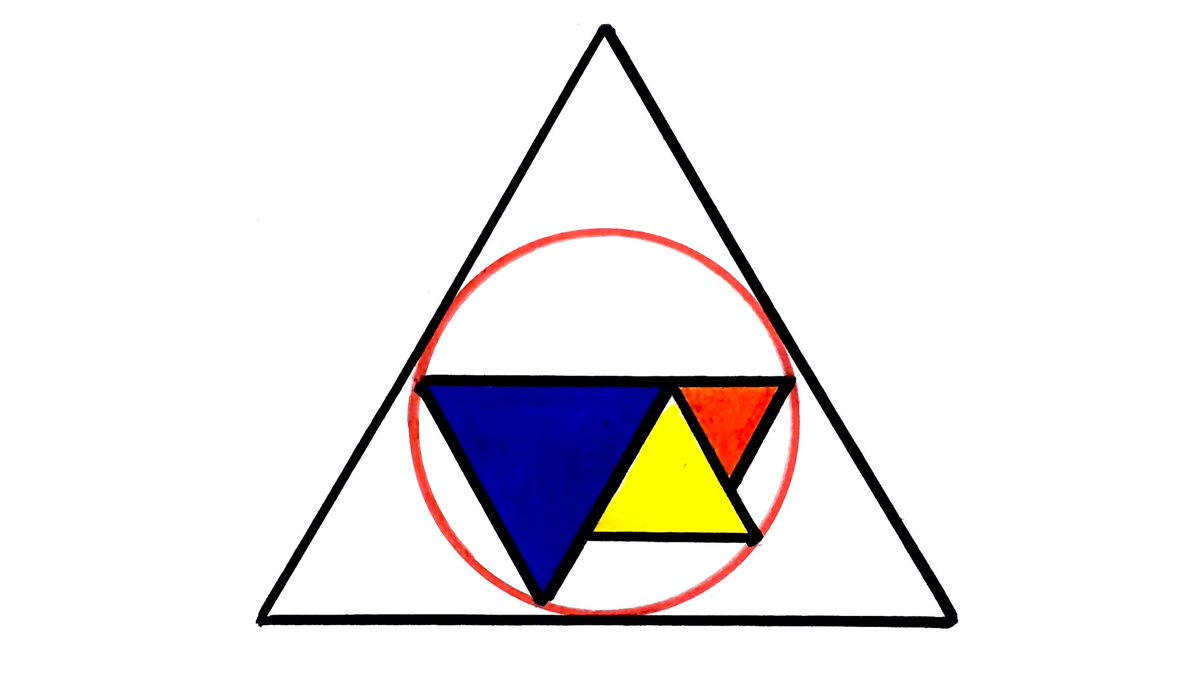
😷 LLAP

[Matthias Apsel]

Hallo Gunnar Bittersmann,

Könnte man sich glatt ein T-Shirt von machen:

Bis demnächst
Matthias

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Wie ist das Verhältnis der schraffierten Fläche der Kreise zur Fläche des Dreiecks für n → ∞?

Man sieht, dass am Rand mehr von Kreisen unbedeckte Fläche bleibt als in der Mitte. Mit wachsendem n schwindet der Einfluss des Randes; für unendlich viele n gibt es keinen Rand mehr. Wir müssen uns also nur die Mitte ansehen; die Ebene wird mit dieser Figur parkettiert:

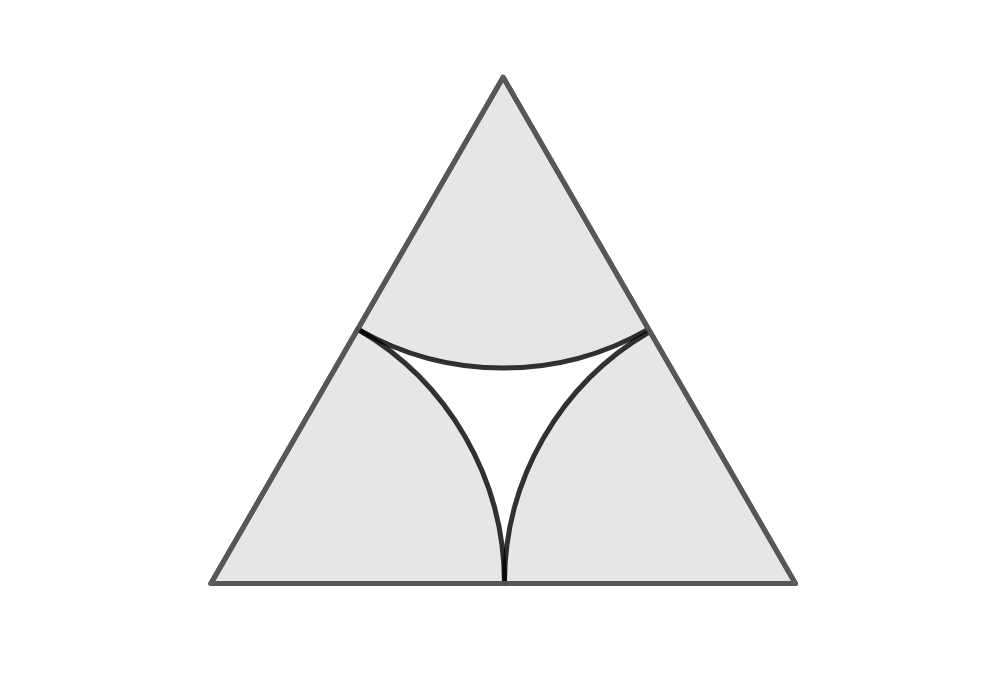
Drei Sechtelkreise machen einen Halbkreis; Fläche ½πr². Die Fläche des gleichseitigen Dreiecks mit Kantenlänge 2r ist r²√3. Das Verhältnis ist also ½π/√3 = ⅙π √3 ≈ 90.69%.

😷 LLAP

PS: Die (allgemeine) Lösung für Aufgabe 2 hab ich auch noch nicht.

[Rolf B]

Hallo Gunnar,

die Idee der Parkettierung hatte ich auch, aber umständlicher mit Trios aus Kreis und Trizoiden (dreicksartige Dinger mit eingebeulten Seiten) die ich zu einer Raute zurecht schiebe. Das braucht zwar ein paar Erklärungen mehr, aber ich komme immerhin auf's gleiche hinaus 😀

Meine Flächenfüllung erfolgt mit diesen Elementen. Zur Flächenberechnung klappe ich wie gezeigt Kreissegmente in die Trizoide hinein und bekomme eine Raute, bestehend aus 2 gleichseitigen Dreiecken der Kantenlänge 2r, Fläche der Raute ist $$A=2\cdot \frac{1}{4}\sqrt 3 (2r)^2 = 2\sqrt3 r^2$$. r² kürzt sich weg, Ergebnis ist das Gleiche wie bei Dir.

Dass Du meine mühsame Argumentation zu den Rändern einfach mit "die Ränder fallen im Unendlichen eh weg" zusammenfasst, tja, so mutig war ich nicht.

Rolf

[ottogal]

Hübsch!

(Erinnert ein bisschen an einen Schnittmusterbogen für eine Mund-Nasen-Maske...)

Dass Du meine mühsame Argumentation zu den Rändern einfach mit "die Ränder fallen im Unendlichen eh weg" zusammenfasst, tja, so mutig war ich nicht.

Finde ich auch etwas kühn...

[Gunnar Bittersmann]

@@ottogal

Dass Du meine mühsame Argumentation zu den Rändern einfach mit "die Ränder fallen im Unendlichen eh weg" zusammenfasst, tja, so mutig war ich nicht.

Finde ich auch etwas kühn...

Ich finde es ausreichend einleuchtend.

Aber wer’s nochmal vorgerechnet haben will:

Die Skizze ist gemalt für N = 3.

Die Ebene eingeteilt in Dreiecke; davon gibt es verschiedene Arten:

weiß:

das Innere. Davon gibt es 1 + 3 + 5 + … + 2N − 1 = N².
Das Verhältnis der Anteil der durch die Kreissektoren bedeckten Fläche ist p₀ = ⅙π √3 ≈ 90.69%.
Die Dreiecke liegen vollständig innerhalb des großen Dreiecks, a₀ = 1.

grün:

an den Kanten. Davon gibt es 3N (von den Dreiecken, nicht von den Kanten).
Das Verhältnis der Anteil der durch die Kreissektoren bedeckten Fläche ist p₁.
Der Anteil des Teilstücks des großen Dreiecks sei a₁.

blau:

an den Kanten. Davon gibt es 3(N + 1).
Das Verhältnis der Anteil der durch die Kreissektoren bedeckten Fläche ist p₂.
Der Anteil des Teilstücks des großen Dreiecks sei a₂.

rot:

an den Ecken. Davon gibt es 3.
Das Verhältnis der Anteil der durch die Kreissektoren bedeckten Fläche ist p₃.
Der Anteil des Teilstücks des großen Dreiecks sei a₃.

baun:

an den Ecken. Davon gibt es 3.
Keine Kreissektoren, p₄ = 0.
Der Anteil des Teilstücks des großen Dreiecks sei a₄.

Das gesuchte Verhältnis p ist nun das gewichtete Mittel

$$p = \frac{N^2 a_0}{N^2 a_0+3Na_1+3(N+1)a_2+3a_3+3a_4}p_0 + \frac{3Na_1}{N^2 a_0+3Na_1+3(N+1)a_2+3a_3+3a_4}p_1 + \frac{3(N+1)a_2}{N^2 a_0+3Na_1+3(N+1)a_2+3a_3+3a_4}p_2 + \frac{3a_3}{N^2 a_0+3Na_1+3(N+1)a_2+3a_3+3a_4}p_3 + \frac{3a_4}{N^2 a_0+3Na_1+3(N+1)a_2+3a_3+3a_4}p_4$$

$$\displaystyle \lim_{N \to \infty}p = p_0 = \tfrac{1}{6}\pi\sqrt{3}$$

Beim Grenzwert bleibt davon nur der erste Summand übrig; die anderen werden zu 0. Der Rand verschwindet, sag ich doch.

Die genauen Werte von p₁, p₂, p₃, a₁, a₂, a₃ und a₄ muss man deshalb gar nicht ermitteln.

😷 LLAP

[Matthias Apsel]

Hallo Gunnar Bittersmann,

Drei Sechtelkreise machen einen Halbkreis; Fläche ½πr². Die Fläche des gleichseitigen Dreiecks mit Kantenlänge 2r ist r²√3. Das Verhältnis ist also ½π/√3 = ⅙π √3 ≈ 90.69%.

Clever!

Bis demnächst
Matthias

[Rolf B]

Hallo Matthias,

auch eine sehr schlaue Idee. Die Berechnung von u kannst Du aber streichen. Lass es einfach als unbekannte Konstante stehen - beim Grenzübergang fliegt es ja eh raus.

Rolf

[ottogal]

Bei $$n$$ Kreisen in der untersten Reihe hat das Dreieck die Seitenlänge $$2 \cdot(n-1+\sqrt{3})$$.

"Betrachtung der Koeffizienten dere quadratischen Glieder" finde ich auch recht verknappt formuliert...

[Matthias Apsel]

Hallo ottogal,

Bei $$n$$ Kreisen in der untersten Reihe hat das Dreieck die Seitenlänge $$2 \cdot(n-1+\sqrt{3})$$.

In der Tat.

"Betrachtung der Koeffizienten dere quadratischen Glieder" finde ich auch recht verknappt formuliert...

Es gibt halt Regeln für die Berechnung von Grenzwerten, die man nicht immer wieder neu zu erläutern braucht.

Bis demnächst
Matthias

[ottogal]

Ich kopier mal meine Lösung von Aufgabe 1 hierher - mit Limes...

[Rolf B]

Hallo Gunnar,

ich habe eine Lösung für Teilaufgabe 2 gefunden.

https://www.geogebra.org/geometry/sx45ckjw

Der Punkt F ist auf der Geraden MO verschiebbar. Der Abstand D (Mittelpunkt des Inkreises) zu F sei Parameter x der Konstruktion, mit Werten von 0 bis r. r ist Radius des Inkreises.

GK ist die Parallele zur Grundlinie durch F. FH die Parallele zu PR durch F. Der Winkel GFH ist demnach 60°. F liegt auf einer Zentralen des Inkreises, daher ist FG=FH und ich habe das gleichseitige Dreieck A. I ist der Schnittpunkt der Parallelen zu QR durch F, und IJ ist die Parallele zur Grundlinie durch I. Damit sind FJ und FI gleich lang und ich habe das gleichseitige Dreieck B. Weil FI und FK parallel zu Geraden liegen, die einen 60° Winkel einschließen, sind die Winkel des orangen Dreiecks C ebenfalls 60°. Es ist gleichseitig, die Konstruktion entspricht der Vorgabe. Jedenfalls mutmaße ich das, die Vorgabe hat ja keinerlei Beschriftung…

Der Sehnensatz besagt, dass das Produkt der Kantenlängen von blauem und orangem Dreieck gleich dem Quadrat der Kantenlänge des grünen Dreiecks ist (weil F auf einer Zentralen des Kreises liegt, ist $$\overline{FI}=\overline{FN}$$).

Es ist also $$ac=b^2$$.

Die Länge von b lässt sich aus x und Kreisradius ableiten: $$x^2+b^2=r^2\Longleftrightarrow b^2=r^2-x^2$$.
Und es ist $$a+c=\overline{GK}$$. An die Länge von GK kommt man auch heran. Der Abstand von F zur Horizontalen durch D sei h. Weil MO um 30° ansteigt, ist h=x/2.
Mit Pythagoras ist

$$\displaystyle h²+\biggl(\frac{\overline{GK}}{2}\biggr)^2=r^2\Longleftrightarrow \overline{GK}^2 = 4(r^2-h^2)=4r^2-x^2$$

Ich habe also 2 Gleichungen mit 2 Unbekannten:

$$ac = r^2-x^2 (=b^2)$$
$$(a+c)^2=4r^2-x^2$$

Hier habe ich eine Weile gehangen. Ich wollte den Stand bis hierher einfach mal ins Forum posten, und habe bei der Gelegenheit genauer hingeguckt!

$$(a+c)^2=a^2+2ac+c^2$$, und wegen $$ac=b^2$$ muss ich davon nur einmal $$ac$$ abziehen, um die Summe $$a^2+b^2+c^2$$ zu erhalten.

$$\displaystyle a^2+b^2+c^2 = 4r^2-x^2 - (r^2-x^2) = 3r^2$$.

Das multipliziere ich mit $$\frac{\sqrt3}{4}$$ und erhalte die Summe der Flächen A,B,C der Teildreiecke!

$$\displaystyle \frac{\sqrt3}{4} a^2+ \frac{\sqrt3}{4} b^2+\frac{\sqrt3}{4}c^2 = A+B+C = \frac{3\sqrt 3}{4} r^2$$.

Hey, juhu, die Summe hängt von x, also von der der Lage von F, nicht ab!

Der Inkreisradius des äußeren Dreiecks ist

$$\displaystyle r=\frac{\overline{PQ}}{2\sqrt3}$$,

das setze ich ein:

$$\displaystyle A+B+C = \frac{3\sqrt 3}{4} \frac{\overline{PQ}^2}{12} = \frac{1}{4}\frac{\sqrt 3}{4} \overline{PQ}^2$$.

Und das ist ein Viertel der Fläche des großen Dreiecks.
Heureka!

Rolf

[Rolf B]

Hallo Rolf,

so, jetzt ist Schluss mit Editieren… Blöde Tipp- und Setzfehler…

Rolf

[Gunnar Bittersmann]

@@Rolf B

so, jetzt ist Schluss mit Editieren…

Lass dir Zeit. Ich schaue mir das eh noch nicht an. Will ja selber noch auf dei Lösung kommen. 🤓

😷 LLAP

[ottogal]

Hallo Rolf,

Chapeau! Feine Lösung.

Ich machte auch den gemeinsamen Eckpunkt der farbigen Dreiecke (bei dir F) auf dem Radius verschiebbar. Da in der Aufgabenstellung weitere Angaben fehlten, vermutete ich, dass die Flächensumme der drei Dreiecke nicht von der Lage von F abhängt. Und in der extremen Lage F = O verschwinden die beiden kleineren, es bleibt nur das blaue mit einem Viertel des Flächeninhalts des großen Dreiecks.

Auch an den Sehnensatz habe ich gedacht - bin aber nicht auf die Gleichungen für x gekommen (Vielleicht, weil man hier oft Stirnrunzeln erzeugt, wenn man den Pythagoras verwendet...?).

Schön, wie du auf $$a^2+b^2+c^2$$ gekommen bist...

Gruß
ottogal

[Rolf B]

Hallo ottogal,

danke. Es war ein mühsamer Weg dahin.

Zuerst wollte ich h als Parameter nehmen und basierend darauf Eckkoordinaten der Dreiecke ausrechnen. Ugh, das war gar nichts.

Dann dachte ich: diese Aufgaben sind meistens basisgeometisch, suchte Hilfslinien, entdeckte die Anwendung des Sehnensatzes und fand meine beiden Gleichungen mit ac und (a+c)².

Damit hatte ich dann versucht, die ac Gleichung nach c aufzulösen und in die (a+c)² Gleichung einzusetzen. Das ergab eine quadratische Gleichung, demnach zwei Lösungen. Und die waren voller Wurzeln. Fast so schlimm wie mein Garten. Immerhin waren die beiden Lösungen laut Geogebra die Werte von a und c, also wohl ohne Rechenfehler. Ich war nur nicht sicher, warum ich, wenn ich die Gleichung für a aufstelle, ich die Lösungen für a UND c bekomme. Vermutlich wegen der Symmetrie der Konstruktion.

$$a_{1/2}=\frac{1}{2}\sqrt{4r^2-x^2}\pm\frac{1}{2}\sqrt 3 x$$ war mir aber zu wüst, um damit weiterzurechnen und x zu eliminieren. Was ich nicht sah und jetzt sehe: Ich hätte für die Flächenberechnung nur $$a_1^2+a_1a_2+a_2^2$$ bilden müssen. Gerade mal gemacht - tatsächlich, da kommt auch 3r² heraus. Egal. Der andere Weg ist deutlich einfacher.

Jedenfalls wollte ich nach Lösung der QuadGl das Teilergebnis posten, um vielleicht Tipps zu bekommen. Und dabei fiel mir auf, dass ich die gewünschte Summe ja eigentlich schon da stehen hatte 😀. Danke an Freund Rainer^[1].

Rolf

---

1. Sein Name ist Zufall. Rainer Zufall. ↩︎

[Gunnar Bittersmann]

@@Rolf B

Ich hab jetzt doch geschmult. 🤷‍♂️

Der Sehnensatz besagt …

Was es nicht alles gibt!

$$\displaystyle a^2+b^2+c^2 = 4r^2-x^2 - (r^2-x^2) = 3r^2$$.

Schöner Lösungsweg.

Das multipliziere ich mit $$\frac{\sqrt3}{4}$$

Brauchst du gar nicht. Am Ende ist das Verhältnis der Flächeninhalte gefragt; und die verhalten sich (bei ähnlichen Figuren, in dem Fall gleichseitigen Dreiecken) wie die Quadrate der Seitenlängen.

Mit $$\overline{PQ} = 2r\sqrt{3}$$ ergibt sich:

$$\displaystyle \frac{a^2+b^2+c^2}{\overline{PQ}^2} = \frac{3r^2}{4r^2 \cdot 3} = \frac{1}{4}$$

😷 LLAP

[Rolf B]

Hallo Gunnar,

Der Sehnensatz besagt …

Was es nicht alles gibt!

Hüstel, Räusper 😈

Mir ging es natürlich genauso, aber ich habe den Satz immerhin nur so weit verdrängt, dass er mir nach 3 Tagen wieder eingefallen ist 😅💦

Rolf

[Matthias Apsel]

Hallo Rolf B,

$$\displaystyle a^2+b^2+c^2 = 4r^2-x^2 - (r^2-x^2) = 3r^2$$.

Bereits hiermit zeigst du, dass die Gesamtfläche unabhängig von x ist.^[1] Insbesondere gilt für den Spezialfall b = c = 0 (Das Dreieck A ist dann dem Kreis einbeschrieben.) a² = 3r².

Unser Kreis ist also gleichzeitig Inkreis des großen Dreiecks und Umkreis des kleinen.

Mit den bekannten oder nachschlagbaren Formeln für Umkreis und Inkreis ergibt sich die Seitenlänge des großen Dreiecks zu 2√3⋅r und die des kleinen zu √3⋅r.

Das gesuchte Verhältnis ist mithin 1:4.

Bis demnächst
Matthias

---

1. Das finde ich übrigens echt bemerkenswert. ↩︎