Dreikönigsmathematik

[Rolf B]

Passend zum Dreikönigstag eine Aufgabe von Catriona Agg mit drei Quadraten. (Vorsicht, im Twitterkanal sind Spoiler).

Catrionas lakonische Aufgabenstellung lautet: "Three squares. What’s the angle?"

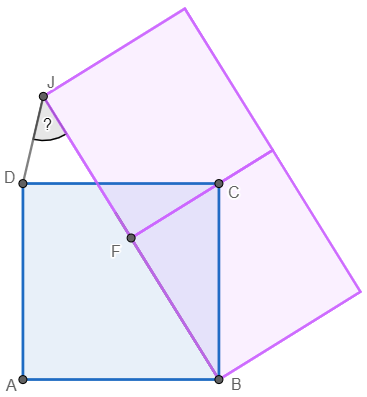
Das Bild habe ich mit Geogebra neu konstruiert. Offensichtlich sind die lilafarbenen Quadrate gleich groß, aber etwas kleiner als das blaue.

Also? Wie groß ist der ?-Winkel bei J?

Rolf

[Rolf B]

Nachtrag 1:

ich habe das Bild gerade einmal durch einen Farbfehlsichtkeits-Simulator laufen lassen (https://barrierefreies.design/barrierefreiheit-interaktiv-testen/farbenfehlsichtigkeit-simulieren), und war etwas schockiert. Blau-Lila ist offenbar eine ungeeignete Kombination.

Lesehilfe: ABCD ist blau, die beiden anderen Quadrate sind lila.

Nachtrag 2:

offensichtlich ist der ?-Winkel von der genauen Lage der lila Quadrate unabhängig, andernfalls wäre eine präzisere Konstruktionsanweisung für das Bild erforderlich.

Ich habe eine Lösung erhalten, die diese Unabhängigkeit voraussetzt und den Winkel an Hand eines Spezialfalles findet. Das sehe ich aber als unvollständig an. Die Lageunabhängigkeit muss sich aus der Lösung ergeben, nicht die Lösung aus der Lageunabhängigkeit.

Rolf

[Der Martin]

Hallo,

ich habe das Bild gerade einmal durch einen Farbfehlsichtkeits-Simulator laufen lassen (https://barrierefreies.design/barrierefreiheit-interaktiv-testen/farbenfehlsichtigkeit-simulieren), und war etwas schockiert. Blau-Lila ist offenbar eine ungeeignete Kombination.

das hätte ich dir auch sagen können. Wir haben ja gestern abend beiläufig den schlechten Kontrast zwischen Rot und Blau erwähnt, und Lila ist eine additive Mischung von Rot und Blau. Mir erscheint es intuitiv klar, dass der Kontrast zwischen X und einer Mischfarbe XY nicht besser sein kann, als zwischen X und Y.

offensichtlich ist der ?-Winkel von der genauen Lage der lila Quadrate unabhängig, andernfalls wäre eine präzisere Konstruktionsanweisung für das Bild erforderlich.

Logisch. 😉

Immer eine Handbreit Wasser unterm Kiel
 Martin

[Rolf B]

Hallo,

Dreikönig ist vorbei und wir haben eine neue Woche. Ich löse mal auf.

Beteiligt haben sich Gunnar, Ottogal und Martin.

Ottogals Lösung ist kurz, knackig und enthält genau das richtige Bild zur Visualisierung. Gunnars Lösung verlief ebenso.

FC ist die Mittelsenkrechte zu BJ; daher ist das Dreieck JBC gleichschenklig.
J liegt somit auf dem Kreis um C durch B und D.
Der gesuchte Winkel ist Umfangswinkel zur Sehne BD in diesem Kreis und daher halb so groß wie der zu ihr gehörende Mittelpunktswinkel DCB - also beträgt er 45°.

Jo, erkennen, dass J auf einem Kreis um C liegt und dann Anwenden des Satzes über Zentri- und Peripheriewinkel - fertig.

Und wenn man den nicht sieht, bricht man sich die Finger. Typisch Catriona Agg eben 😀

Martin hat es etwas anders gelöst. Offenbar ist der Winkel nicht von der Lage der lila Quadrate abhängig, sonst gäbe es in der Aufgabe einen Hinweis auf die genaue Lage. Also hat er die Lage so gewählt, dass F und C zusammenfallen - und dann sind die 45° offensichtlich. Diese Vorgehensweise ist pragmatisch, aber irgendwie fühlt es sich gemogelt an 😉

Rolf

[Der Martin]

Hallo Rolf,

FC ist die Mittelsenkrechte zu BJ; daher ist das Dreieck JBC gleichschenklig.
J liegt somit auf dem Kreis um C durch B und D.
Der gesuchte Winkel ist Umfangswinkel zur Sehne BD in diesem Kreis und daher halb so groß wie der zu ihr gehörende Mittelpunktswinkel DCB - also beträgt er 45°.

Jo, erkennen, dass J auf einem Kreis um C liegt und dann Anwenden des Satzes über Zentri- und Peripheriewinkel - fertig.

von diesem Satz habe ich noch nie gehört. Das wäre bei mir wieder ein Fall gewesen wie: "Man erkennt deutlich [...], aber man ich kann es nicht schlüssig begründen."

Martin hat es etwas anders gelöst. Offenbar ist der Winkel nicht von der Lage der lila Quadrate abhängig, sonst gäbe es in der Aufgabe einen Hinweis auf die genaue Lage. Also hat er die Lage so gewählt, dass F und C zusammenfallen - und dann sind die 45° offensichtlich. Diese Vorgehensweise ist pragmatisch, aber irgendwie fühlt es sich gemogelt an 😉

Pragmatismus ist immer meine bevorzugte Strategie. Und ein bisschen Mogeln ist auch okay, solange es nicht klar gegen die Regeln ist.

Pragmatisch war ich auch schon bei meiner Diplomarbeit. Die Aufgabe war, einen Regler in Software zu implementieren, der in einem Oberklasse-PKW anhand des invertierten mathematischen Modells des Antriebsstrangs und der Längsdynamik die Stellgrößen für Bremse und Gas (Automatik-Fahrzeug) bestimmt, mit denen eine vorgegebene Geschwindigkeit oder Beschleunigung erreicht wird.
Mein Betreuer war ein Professor, der Regelungstechnik als sein Schwerpunktthema hatte. Ich hatte immer wieder Mühe, ihm klarzumachen, dass man in Software auch Unstetigkeiten, adaptive Parameter oder andere Schmankerln realisieren kann, die sich mit der klassischen Regelungstechnik nicht abbilden lassen.
Am meisten störte ihn, glaube ich, dass ich um des Fahrkomforts willen die Stellgrößen für Gaspedal und Bremse nochmal über einen adaptiven Tiefpass laufen ließ. "Das macht man aber nicht!"

Letzten Endes kam aber doch eine 1.6 als Diplomnote dabei raus.

Immer eine Handbreit Wasser unterm Kiel
 Martin

[Der Martin]

n'Abend,

ich habe eben nochmal versucht, die "Musterlösung" nachzuvollziehen.

FC ist die Mittelsenkrechte zu BJ; daher ist das Dreieck JBC gleichschenklig.

Okay, bis dahin kann ich folgen.

J liegt somit auf dem Kreis um C durch B und D.

Wieso? Wo ist der Zusammenhang? [EDIT: Okay, das habe ich inzwischen erkannt.]

Der gesuchte Winkel ist Umfangswinkel zur Sehne BD in diesem Kreis und daher halb so groß wie der zu ihr gehörende Mittelpunktswinkel DCB - also beträgt er 45°.

Da hast du mich ganz klar verloren.

Jo, erkennen, dass J auf einem Kreis um C liegt und dann Anwenden des Satzes über Zentri- und Peripheriewinkel - fertig.

Und wenn man den nicht sieht, bricht man sich die Finger. Typisch Catriona Agg eben 😀

Entweder sehe ich den Wald vor lauter Bäumen nicht, oder mir fehlen elementare Grundkenntnisse. Oder auch beides.

Immer eine Handbreit Wasser unterm Kiel
 Martin

[Rolf B]

Hallo Martin,

den verlinkten Wikipedia-Artikel hast Du gelesen?

Schau Dir das Bild https://commons.wikimedia.org/wiki/File:Kreiswinkel.svg nochmal an - es zeigt die 3 möglichen Fälle und ich werde mich jetzt darauf beziehen. Fall 2 ist ein Sonderfall und wird in der Schule als Satz des Thales gelehrt. Der Sehnentangentenwinkel $$\tau$$ ist für die Aufgabe irrelevant, den lassen wir weg.

Ausgangsbasis für den allgemeinen Fall ist ein Kreissektor, also das Tortenstück mit Spitze bei M und den Punkten A und B auf dem Kreis, die den Sektor begrenzen. Dieser Kreissektor hat einen Öffnungswinkel µ. Das Tortenstück kann kleiner als die Hälfte der Torte sein (Fall 1), gleich groß oder - mjam! - größer (Fall 3).

Jetzt legen wir einen Punkt P auf den Umfang vom Tortenrest, und betrachten zwei Winkel: Den Zentriwinkel (oder Mittelpunktswinkel) - das ist der blaue Öffnungswinkel des Tortenstücks. Und den Peripheriewinkel (oder Umfangswinkel) - das ist der rote Winkel von den Ecken A und B des Tortenstücks zum Punkt P.

Die Beobachtung ist, dass der Winkel bei P immer gleich groß ist, egal wo P auf dem Tortenrest liegt, und dass er halb so groß ist wie der Zentriwinkel bei M. Der Beweis dafür steht im Wikipedia-Artikel.

Übertragen wir das jetzt auf die Aufgabe von Catriona. Die Torte ist der Kreis um C, das Tortenstück geht (in Linksdrehung) von D nach B. Es hat einen Zentriwinkel von 90°. Der Tortenrest ist der Dreiviertelkreis von B nach D und J ist ein Punkt auf dem Umfang des Tortenrests. Demnach ist der Winkel bei J halb so groß wie der Zentriwinkel - 45°.

Rolf

[Der Martin]

Hallo,

den verlinkten Wikipedia-Artikel hast Du gelesen?

ja, so gut ich konnte. Das fällt mir bei solchem Mathe-Kram immer schwer.

Fall 2 ist ein Sonderfall und wird in der Schule als Satz des Thales gelehrt.

Der ist mir auch geläufig.

Die Beobachtung ist, dass der Winkel bei P immer gleich groß ist, egal wo P auf dem Tortenrest liegt, und dass er halb so groß ist wie der Zentriwinkel bei M. Der Beweis dafür steht im Wikipedia-Artikel.

Dass er bei gegebenem µ immer gleich ist, kann ich noch nachvollziehen. Aber warum er ausgerechnet halb so groß ist, habe ich immer noch nicht kapiert.

Aber das ist mir jetzt auch egal; ich betrachte Mathematik allgemein als Hilfsmittel, und nicht als Selbstzweck oder etwas, was man zum Spaß macht. Mir genügt es, wenn ich in gewissen Situationen weiß, "das ist so", und um das "warum" dürfen sich gern andere kümmern bzw. gekümmert haben.

Immer eine Handbreit Wasser unterm Kiel
 Martin

[Tabellenkalk]

Hallo,

Und wenn man den nicht sieht, bricht man sich die Finger. Typisch Catriona Agg eben 😀

In der Aufgabe den Kreis einfach wegzulassen, ist aber ganz schön fies! !😠

Martin hat es etwas anders gelöst. Offenbar ist der Winkel nicht von der Lage der lila Quadrate abhängig, sonst gäbe es in der Aufgabe einen Hinweis auf die genaue Lage. Also hat er die Lage so gewählt, dass F und C zusammenfallen - und dann sind die 45° offensichtlich. Diese Vorgehensweise ist pragmatisch, aber irgendwie fühlt es sich gemogelt an 😉

So hatte ich es auch...
Blöd ist das nur, wenn der Winkel variabel und als Lösung eine Funktion gesucht wäre.

Gruß
Kalk

[Rolf B]

Hallo Tabellenkalk,

wenn der Winkel variabel und als Lösung eine Funktion gesucht wäre

dann würde ich annehmen, dass Catriona die Aufgabe anders formulieren würde. Bisher waren ihre Aufgaben auch immer eindeutig, meine ich.

den Kreis wegzulassen ist fies

Hihi - die Aufgaben sind ja auch nicht dazu gedacht, dass man ihre Lösung tanzen kann (mit einem respektvollen Blick zu allen Steiner-Opfern, die mehr können als ihren Namen zu tanzen)

Rolf

[ottogal]

Ja, ich mag es gern kurz und knackig - und das heißt halt, dass man manchmal einen nicht ganz so elementaren Satz heranzieht...

Aber so mag es ja Catriona Agg auch in ihren Fragestellungen - die Voraussetzungen spricht sie nicht alle aus (man "sieht" sie schon...).

Hier sind es ja nicht einfach 3 Quadrate. Sie liegen in ganz bestimmter Weise zueinander, aber nicht eindeutig: Die gemeinsame Seite der beiden kleineren Quadrate muss durch die Ecke C des größeren Quadrats gehen.

Worauf kommt es also an? Dass das Dreieck BCF bei F einen rechten Winkel hat.

Bei dem Stichwort sollte einem immer der Satz von Thales einfallen (der ihm natürlich nicht als Spezialfall des Peripheriewinkelsatzes untergekommen ist, sondern wohl schlicht anhand der Symmetrien eines Rechtecks mit Umkreis).

Somit liegt F auf dem Thales(halb)kreis über BC.

Nun verwenden wir wieder das gehabte Argument: Der Winkel EFB ist Peripheriewinkel zur Sehne EB des Thaleskreises. Deren Mittelpunktswinkel ist ein rechter, folglich hat EFB 45°.

Und dann braucht man nur zu "sehen", dass das Dreieck DJB das Bild des Dreiecks EFB bei der Zentrischen Streckung mit Zentrum B und Streckfaktor 2 ist, und zu wissen, dass dies eine winkeltreue Abbildung ist... (Oder man macht zuerst die Streckung und argumentiert im Kreis um C wie gehabt.)

[Rolf B]

Hallo ottogal,

ich hab jetzt eine Weile grübeln müssen, um zu verstehen, was Du da erklärst. Die zentrische Streckung muss man erstmal innerlich verargumentieren (zwei Seiten verdoppeln sich, der Winkel dazwischen bleibt gleich -> Ähnlichkeit). Ist das nicht viel zu umständlich?

Dass BFC ein rechter Winkel ist, ergibt sich aus der Tatsache, dass es eine Quadratecke ist. Das zu sehen, braucht nicht viel. Der entscheidende Schritt ist meiner Meinung nach, die Linie JC zu zeichnen, denn dann sieht man sehr schnell, dass JBC gleichschenklig ist und kann auf die Idee kommen, dass B,D und J auf einem Kreis um C liegen. Und dann muss einem natürlich der Peripheriewinkelsatz einfallen - aber wenn man erstmal auf die Idee mit dem Hilfskreis gekommen ist, findet man auch den Weg zu einer Liste mit gängigen Lehrsätzen über Kreissehnen und ihre Beziehungen.

Rolf

[ottogal]

Ist das nicht viel zu umständlich?

Ja, schon. Das sollte auch nur meinen ursprünglichen Gedankengang wiedergeben. Zum "kurz und knackig" kam ich erst durch die Selbstanfrage "Gehts nicht weniger umständlich?"... 🙃