Mathematik zum Wochenende – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

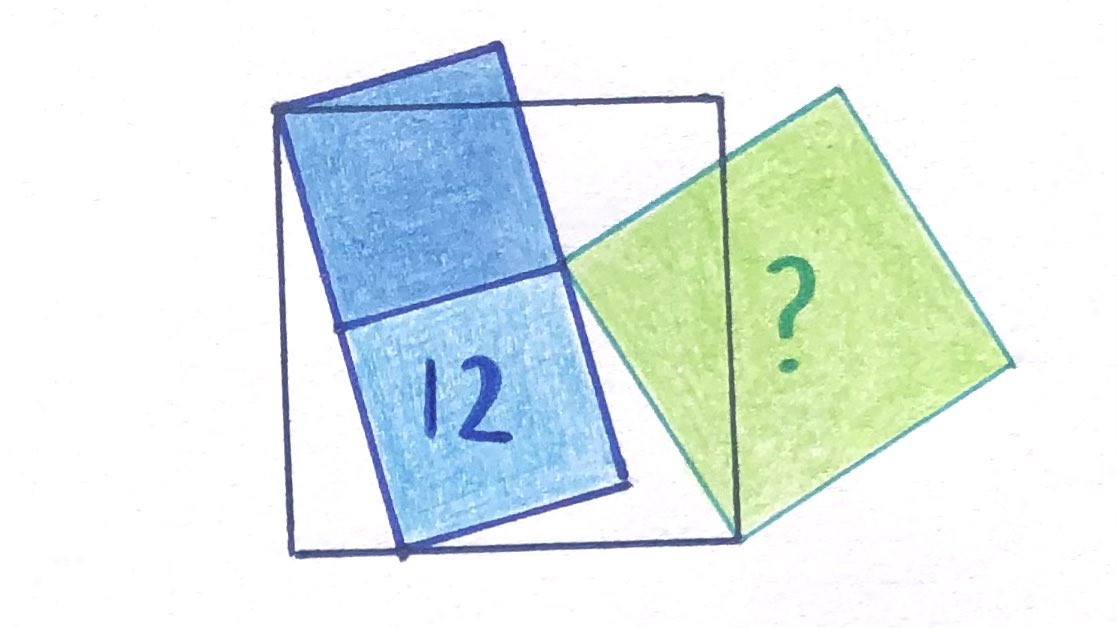
Vier Quadrate. Wie groß ist die grüne Fläche?

Da hat sich die Teilnahme am SELFHTML-Treffen doch gelohnt! Beim Sachenpacken hab ich im Rucksack einen Zettel mit der Skizze der Lösung gefunden, die ich schon wieder vergessen hatte.

Auch die Lösung von @ottogal ging so, aber auch seine Skizze ging mir verloren.

Bezeichnungen von Längen und Punkten:

Die beiden schraffierten Dreiecke sind nach WSW kongruent (rechte Winkel, Hypotenusen sind Quadratseiten, und wie man leicht sieht, sind auch die gekennzeichneten Winkel gleich).

Damit ist AQ = PQ = a + b

BQ = AB − AQ = 2a − (a + b) = a − b

Pythagogas:
x² = a² + b²

y² = (a + b)² + (a − b)² = 2a² + 2b² = 2x²

Das grüne Quadrat ist also doppelt so groß wie eins der kleinen Quadrate, d.h. ebenso groß wie die blaue Fläche: 12.

Nachtrag: Bzw. 24 – je nachdem, wie man die Aufgabe versteht.

Die Aufgabe stammte mal wieder aus einem Tweet von Catriona Agg.

Kwakoni Yiquan