Mathematik zum Wochenende
- mathematik
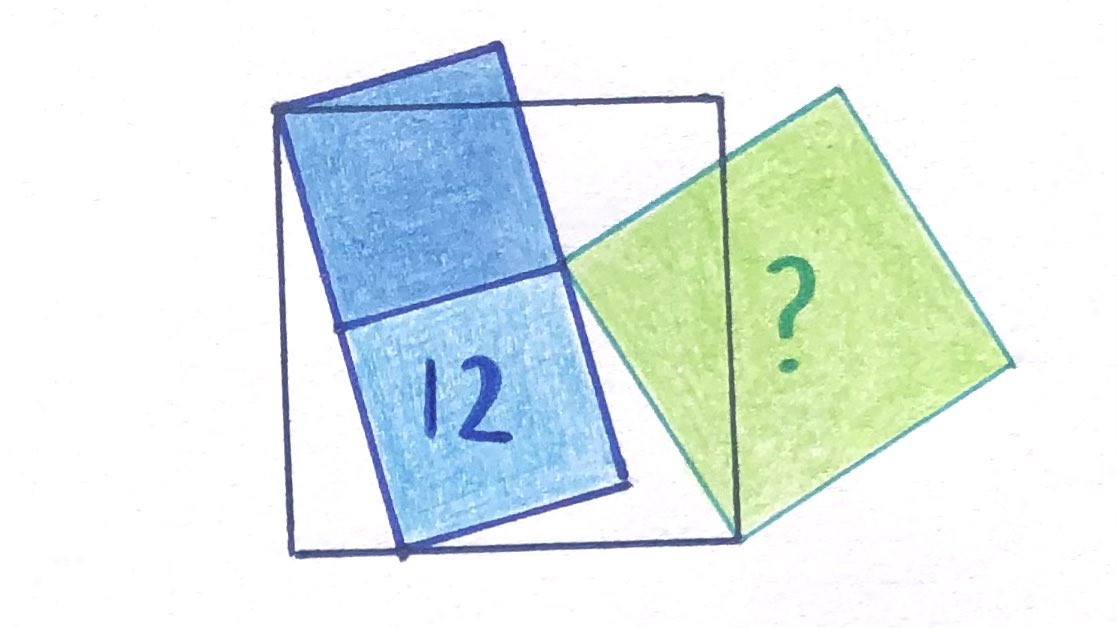
Vier Quadrate. Wie groß ist die grüne Fläche?
Kwakoni Yiquan
Hi there,
Vier Quadrate. Wie groß ist die grüne Fläche?
Keine Ahnung, aber die andere blaue Fläche könnte 12 sein...😛
@@klawischnigg
Vier Quadrate. Wie groß ist die grüne Fläche?
Keine Ahnung, aber die andere blaue Fläche könnte 12 sein...😛
YMMD. 😂
Kwakoni Yiquan
@@klawischnigg
Vier Quadrate. Wie groß ist die grüne Fläche?
Keine Ahnung, aber die andere blaue Fläche könnte 12 sein...😛
YMMD. 😂
Sehr fein.
Im Ernst - wäre es für Dich eine Lösung, wenn ich die Vermutung äußere, daß die Seitenlänge des grünen Quadrats ident zu sein scheint mit der Diagonale des blauen Quadrates oder oder ist das jetzt ein Zufall und somit zu trivial (wie ich fast befürchte...😉)
@@klawischnigg
Im Ernst - wäre es für Dich eine Lösung, wenn ich die Vermutung äußere, daß die Seitenlänge des grünen Quadrats ident zu sein scheint mit der Diagonale des blauen Quadrates
Eine Lösung wäre es, wenn du das nicht nur vermutest, sondern auch begründest. Hieb- und stichfest.
Und das nicht hier im Thread, sondern per DM an mich. Sonst stellen wir deine Hieb- und Stichfestigkeit auf die Probe. 😜
Kwakoni Yiquan
Hi there,
Eine Lösung wäre es, wenn du das nicht nur vermutest, sondern auch begründest. Hieb- und stichfest.
Und das nicht hier im Thread, sondern per DM an mich. Sonst stellen wir deine Hieb- und Stichfestigkeit auf die Probe. 😜
verstanden und verinnerlicht...
@@Gunnar Bittersmann
Vier Quadrate. Wie groß ist die grüne Fläche?
Da hat sich die Teilnahme am SELFHTML-Treffen doch gelohnt! Beim Sachenpacken hab ich im Rucksack einen Zettel mit der Skizze der Lösung gefunden, die ich schon wieder vergessen hatte.
Auch die Lösung von @ottogal ging so, aber auch seine Skizze ging mir verloren.
Bezeichnungen von Längen und Punkten:
Die beiden schraffierten Dreiecke sind nach WSW kongruent (rechte Winkel, Hypotenusen sind Quadratseiten, und wie man leicht sieht, sind auch die gekennzeichneten Winkel gleich).
Damit ist AQ = PQ = a + b
BQ = AB − AQ = 2a − (a + b) = a − b
Pythagogas:
x² = a² + b²
y² = (a + b)² + (a − b)² = 2a² + 2b² = 2x²
Das grüne Quadrat ist also doppelt so groß wie eins der kleinen Quadrate, d.h. ebenso groß wie die blaue Fläche: 12.
Nachtrag: Bzw. 24 – je nachdem, wie man die Aufgabe versteht.
Die Aufgabe stammte mal wieder aus einem Tweet von Catriona Agg.
Kwakoni Yiquan
Das grüne Quadrat ist also doppelt so groß wie eins der kleinen Quadrate, d.h. ebenso groß wie die blaue Fläche: 12.
?? In Catrionas Skizze ist doch 12 die Fläche von 1 blauen Quadrat.
@@ottogal
Das grüne Quadrat ist also doppelt so groß wie eins der kleinen Quadrate, d.h. ebenso groß wie die blaue Fläche: 12.
?? In Catrionas Skizze ist doch 12 die Fläche von 1 blauen Quadrat.
Ist sie das?
Ich glaube, damals dachte ich das auch. Heute sah ich es anders. Kann man so oder so sehen.
Wie dem auch sei, die Lösung ist: grün gleich blau.
Kwakoni Yiquan
Es geht noch viel einfacher:
(Ergänze Bezeichnungen C, D für Quadrat ABCD.)
Wegen AQ = PQ = a+ b liegt P auf der Quadratdiagonalen AC.
Es folgt PB = PD.
Die Seite des grünen Quadrats ist also so lang wie die Diagonale des (oberen) blauen Quadrats. Es hat also den doppelten Flächeninhalt wie dieses.
@@ottogal
Es geht noch viel einfacher:
Ich hätte mir deine DM (auch ohne Skizze) nochmal ansehen sollen.
Kwakoni Yiquan
Warum ist eigentlich meine eingefügte Skizze hier nicht mehr aufrufbar?
Hallo ottogal,
im Audit-Log finde ich, dass User ottogal am 26.02. um 09:03 Uhr ein 7cdc637e-d47d-11ee-a0de-9c6b00263d9f.png erstellt hat. Es ist am 12.03. um 0:00 Uhr gelöscht worden, also Mitternacht nach 14 Tagen. Das dürfte ein Cleanup-Job gewesen sein.
Bist Du der Auffassung, dass das Bild zu dieser Zeit noch irgendwo verlinkt war? Dann wär's ein Bug.
Rolf
Bist Du der Auffassung, dass das Bild zu dieser Zeit noch irgendwo verlinkt war? Dann wär's ein Bug.
Das kann ich nicht mehr sagen. Es war nur für die PM gedacht, aber die aktuelle Wiederaufnahme einer alten Diskussion zeigt, dass dieses frühe "Clearen" von Bildern in PMs schlecht ist. Auch wird es einem so schon nur durch einen Trick möglich, ein Bild in eine PM einzufügen. Weshalb tut das not? Soviel Datenstrom entsteht doch dadurch nicht.
Hallo ottogal,
das Forum hält nach, ob ein Bild verwendet wird oder nicht. Unbenutzte Bilder werden gelöscht. Gründe:
Es ist schon doof, wenn man als Dienstanbieter prinzipiell mit einem Bein im Knast steht.
Rolf
Hallo Rolf,
vielen Dank für die Erläuterung der nachvollziehbaren Gründe!
ottogal
Hallo,
hab mir erlaubt, die „Diagonale“ zu ergänzen…
Gruß
Kalk